
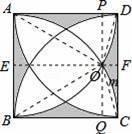
如圖,正方形ABCD的邊長為2,四條弧分別以相應頂點為圓心,正方形ABCD的邊長為半徑.求陰影部分的面積 .


16﹣4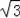
 ﹣
﹣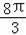
 .
.
【考點】扇形面積的計算;正方形的性質.
【專題】幾何圖形問題.
【分析】如解答圖,作輔助線,利用圖形的對稱性求解.解題要點是求出弓形OmC的面積.
【解答】解:如圖,設點O為弧的一個交點.
連接OA、OB,則△OAB為等邊三角形,∴∠OBC=30°.
過點O作EF⊥CD,分別交AB、CD于點E、F,則OE為等邊△OAB的高,
∴OE=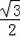
 AB=
AB=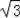
 ,∴OF=2﹣
,∴OF=2﹣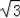
 .
.
過點O作PQ⊥BC,分別交AD、BC于點P、Q,則OQ=1.
S弓形OmC=S扇形OBC﹣S△OBC=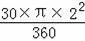
 ﹣
﹣
 ×2×1=
×2×1=
 ﹣1.
﹣1.
∴S陰影=4(S△OCD﹣2S弓形OmC)=4[
 ×2×(2﹣
×2×(2﹣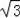
 )﹣2(
)﹣2(
 ﹣1)]=16﹣4
﹣1)]=16﹣4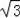
 ﹣
﹣
 .
.
故答案為:16﹣4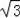
 ﹣
﹣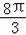
 .
.

【點評】本題考查了扇形的面積公式和正方形性質的+應用,主要考查學生的計算能力,題目比較好,難度不大.


 優百分課時互動系列答案
優百分課時互動系列答案科目:初中數學 來源: 題型:
如圖,小明用鉛筆可以支起一張質地均勻的三角形卡片,則他支起的這個點應是三角形的( )
A.三邊高的交點 B.三條角平分線的交點
C.三邊垂直平分線的交點 D.三邊中線的交點

查看答案和解析>>
科目:初中數學 來源: 題型:
某班組織活動,班委會準備用15元錢全部用來購買筆記本和中性筆兩種獎品.已知筆記本2元/本,中性筆1元/支,且每種獎品至少買一件.
(1)有多少種購買方案?請列舉所有可能的結果;
(2)從上述方案中任選一種方案購買,求買到的中性筆數量多于筆記本數量的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
一個不透明的口袋中裝有4個分別標有數字﹣1,﹣2,3,4的小球,它們的形狀、大小完全相同.小紅先從口袋中隨機摸出一個小球記下數字為x;小穎在剩下的3個小球中隨機摸出一個小球記下數字為y.
(1)小紅摸出標有數字3的小球的概率是 ;
(2)請用列表法或畫樹狀圖的方法表示出由x,y確定的點P(x,y)所有可能的結果;
(3)若規定:點P(x,y)在第一象限或第三象限小紅獲勝;點P(x,y)在第二象限或第四象限則小穎獲勝.請分別求出兩人獲勝的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
在初三基礎測試中,我學校的小明的6科成績分別為語文118分,英語117分,數學117分,物理83分,化學80分,政治83分,則他的成績的眾數為 分.
查看答案和解析>>
科目:初中數學 來源: 題型:
2012年5月8日,“最美教師”張麗莉為救學生身負重傷,張老師舍己救人的事跡受到全國人民的極大關注,在住院期間,共有695萬人以不同方式向她表示問候和祝福,將695萬人用科學記數法表示為 人.(結果精確到十萬位)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com