一個不透明的口袋中裝有4個分別標有數字﹣1，﹣2，3，4的小球，它們的形狀、大小完全相同．小紅先從口袋中隨機摸出一個小球記下數字為x；小穎在剩下的3個小球中隨機摸出一個小球記下數字為y．
（1）小紅摸出標有數字3的小球的概率是 ；
（2）請用列表法或畫樹狀圖的方法表示出由x，y確定的點P（x，y）所有可能的結果；
（3）若規定：點P（x，y）在第一象限或第三象限小紅獲勝；點P（x，y）在第二象限或第四象限則小穎獲勝．請分別求出兩人獲勝的概率．
【考點】列表法與樹狀圖法．
【專題】計算題．
【分析】（1）直接根據概率公式求解；
（2）通過列表展示所有12種等可能性的結果數；
（3）找出在第一象限或第三象限的結果數和第二象限或第四象限的結果數，然后根據概率公式計算兩人獲勝的概率．
【解答】解：（1）小紅摸出標有數字3的小球的概率是
；
故答案為；
（2）列表如下：
| ﹣1 | ﹣2 | 3 | 4 | |
| ﹣1 | （﹣1，﹣2） | （﹣1，3） | （﹣1，4） | |
| ﹣2 | （﹣2，﹣1） | （﹣2，3） | （﹣2，4） | |
| 3 | （3，﹣1） | （3，﹣2） | （3，4） | |
| 4 | （4，﹣1） | （4，﹣2） | （4，3） |
（3）從上面的表格可以看出，所有可能出現的結果共有12種，且每種結果出現的可能性相同，其中點（x，y）在第一象限或第三象限的結果有4種，第二象限或第四象限的結果有8種，
所以小紅獲勝的概率=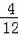
=
，小穎獲勝的概率=
=
．
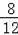
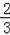
【點評】本題考查了列表法或樹狀圖法：通過列表法或樹狀圖法展示所有等可能的結果求出n，再從中選出符合事件A或B的結果數目m，然后根據概率公式求出事件A或B的概率．
科目：初中數學 來源： 題型：
已知某市2014年企業用水量x（噸）與該月應交的水費y（元）之間的函數關系如圖．
（1）當x≥50時，求y關于x的函數關系式；
（2）若某企業2014年10月份的水費為620元，求該企業2014年10月份的用水量；
（3）為鼓勵企業節約用水，該市自2015年1月開始對月用水量超過80噸的企業加收污水處理費，規定：若企業月用水量x超過80噸，則除按2014年收費標準收取水費外，超過80噸的部分每噸另加收
元的污水處理費，若某企業2015年3月份的水費和污水處理費共600元，求這個企業3月份的用水量．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
； 
B．
C．