
【題目】定義:如點M、N把線段AB分割成AM、MN、BN,若以AM、MN、BN,為邊的三角形是一個直角三角形,則稱點M、N是線段AB的勾股分割點.
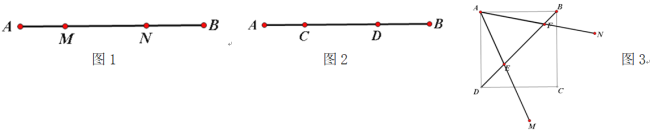
(1)如圖2,已知點C、D是線段AB的勾股分割點,若AC=3,DB=4,求CD的長;
(2)如圖3,在正方形ABCD中,∠MAM=45°,角的兩邊AM、AN分別交BD于E、F(不與端點重合),求證:E、F是BD的勾股分割點.
【答案】(1)5或![]() .(2)證明過程見解析.
.(2)證明過程見解析.
【解析】
(1)①當CD為最大線段時,由勾股定理求出CD的長;②當BD為最大線段時,由勾股定理求出CD即可;
(2)將△ABF繞點A順時針旋轉90°得到△ADH,連接HE,只要證明△EAH≌△EAF,推出EF=HE,再證明∠HDE=90°即可.
(1)解:①當CD為最大線段時,
∵點C、D是線段AB的勾股分割點
∴CD=![]() =
=![]() =5
=5
②當BD為最大線段時,
∵點C、D是線段AB的勾股分割點
∴CD=![]() =
=![]() =
=![]()
綜上,CD的長為5或![]() .
.
(2)證明:如圖,將△ABF繞點A順時針旋轉90°得到△ADH,連接HE

∵∠BAF+∠DAE=90°-∠MAN=90°-45°=45°,∠BAF=∠DAH
∴∠DAH+∠DAE=45°
即∠EAH=45°
在△EAH和△EAF中

∴△EAH≌△EAF(SAS)
∴EH=EF
∵四邊形ABCD為正方形,BD為對角線
∴∠ABF=∠ADB=45°
∴∠ADH=∠ABF=∠ADB =45°
∴∠HDE=90°
在Rt△DHE中,HE2=DH2+DE2
∵DH=BF,EF=HE
∴EF2=BF2+DE2
∴E、F是BD的勾股分割點.


科目:初中數學 來源: 題型:
【題目】生活與數學
日 | 一 | 二 | 三 | 四 | 五 | 六 |
1 | 2 | 3 | 4 | 5 | 6 | |
7 | 8 | 9 | 10 | 11 | 12 | 13 |
14 | 15 | 16 | 17 | 18 | 19 | 20 |
21 | 22 | 23 | 24 | 25 | 26 | 27 |
(1)姆同學在某月的日歷上圈出2×2個數,正方形的方框內的四個數的和是48,那么這四個數是_______.
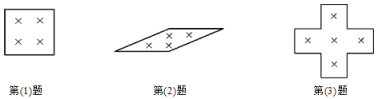
(2)麗也在上面的日歷上圈出2×2個數,斜框內的四個數的和是46,則它們分別是_____.
(3)莉也在日歷上圈出5個數,呈十字框形,它們的和是55,則中間的數是______.
(4)某月有5個星期日的和是75,則這個月中最后一個星期日是______號?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,Rt△ABC中,∠C=90°,把R△ABC繞著B點逆時針旋轉,得到Rt△DBE,點E在AB上 .
(1)若∠BDA=70°,求∠BAC的度數;
(2)若BC=8,AC=6,求△ABD中AD邊上的高.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下面材料:
在數軸上5與﹣2所對的兩點之間的距離:|5﹣(﹣2)|=7;
在數軸上﹣2與3所對的兩點之間的距離:|﹣2﹣3|=5;
在數軸上﹣8與﹣5所對的兩點之間的距離:|(﹣8)﹣(﹣5)|=3
在數軸上點A、B分別表示數a、b,則A、B兩點之間的距離AB=|a﹣b|=|b﹣a|
回答下列問題:
(1)數軸上表示﹣2和﹣5的兩點之間的距離是_____;
數軸上表示數x和3的兩點之間的距離表示為_____;
數軸上表示數_____和_____的兩點之間的距離表示為|x+2|,;
(2)七年級研究性學習小組在數學老師指導下,對式子|x+2|+|x﹣3|進行探究:
①請你在草稿紙上畫出數軸,當表示數x的點在﹣2與3之間移動時,|x﹣3|+|x+2|的值總是一個固定的值為:_____.
②請你在草稿紙上畫出數軸,要使|x﹣3|+|x+2|=7,數軸上表示點的數x=_____.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知△ABC,以AC為邊在△ABC外作等腰△ACD,其中AC=AD
(1) 如圖1,若AB為邊在△ABC外作△ABE,AB=AE,∠DAC=∠EAB=60°,求∠BFC的度數
(2) 如圖2,∠ABC=α,∠ACD=β,BC=6,BD=8
① 若α=30°,β=60°,AB的長為
② 若改變α、β的大小,但α+β=90°,求△ABC的面積
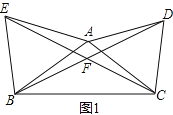
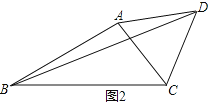
查看答案和解析>>
科目:初中數學 來源: 題型:
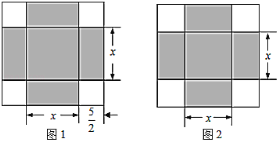
【題目】《代數學》中記載,形如![]() 的方程,求正數解的幾何方法是:“如圖1,先構造一個面積為
的方程,求正數解的幾何方法是:“如圖1,先構造一個面積為![]() 的正方形,再以正方形的邊長為一邊向外構造四個面積為
的正方形,再以正方形的邊長為一邊向外構造四個面積為![]() 的矩形,得到大正方形的面積為
的矩形,得到大正方形的面積為![]() ,則該方程的正數解為
,則該方程的正數解為![]() .”小聰按此方法解關于
.”小聰按此方法解關于![]() 的方程
的方程![]() 時,構造出如圖2所示的圖形,已知陰影部分的面積為36,則該方程的正數解為( )
時,構造出如圖2所示的圖形,已知陰影部分的面積為36,則該方程的正數解為( )
A.6B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
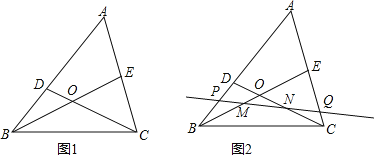
【題目】如圖,在![]() 中,D、E分別為AB、AC上的點,線段BE、CD相交于點O,且
中,D、E分別為AB、AC上的點,線段BE、CD相交于點O,且![]() .
.
![]() 求證:
求證: ![]() ∽
∽![]() ;
;
![]() 求證:
求證: ![]() ;
;
![]() 若M、N分別是BE、CD的中點,過MN的直線交AB于P,交AC于Q,線段AP、AQ相等嗎?為什么?
若M、N分別是BE、CD的中點,過MN的直線交AB于P,交AC于Q,線段AP、AQ相等嗎?為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】制作一種產品,需先將材料加熱達到60 ℃后,再進行操作.設該材料溫度為y(℃),從加熱開始計算的時間為x(min).據了解,當該材料加熱時,溫度y與時間x成一次函數關系;停止加熱進行操作時,溫度y與時間x成反比例關系(如圖).已知該材料在操作加熱前的溫度為15 ℃,加熱5分鐘后溫度達到60 ℃.

(1)分別求出將材料加熱和停止加熱進行操作時,y與x的函數關系式;
(2)根據工藝要求,當材料的溫度低于15 ℃時,須停止操作,那么從開始加熱到停止操作,共經歷了多少時間?
查看答案和解析>>
科目:初中數學 來源: 題型:
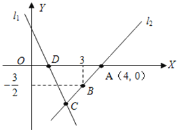
【題目】如圖,直線![]() 的解析表達式為
的解析表達式為![]() ,且
,且![]() 與x軸交于點D,直線
與x軸交于點D,直線![]() 經過點A,點B,直線
經過點A,點B,直線![]() ,
,![]() 交于點C.
交于點C.
(1)求直線![]() 的解析表達式;
的解析表達式;
(2)求![]() 的面積;
的面積;
(3)在直線![]() 上存在異于點C的另一點P,使得
上存在異于點C的另一點P,使得![]() 的面積等于
的面積等于![]() 面積,請直接寫出點P的坐標.
面積,請直接寫出點P的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com