
題目列表(包括答案和解析)
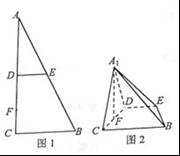
如圖1,在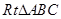 中,
中,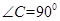 ,D,E分別為AC,AB的中點,點F為線段CD上的一點,將
,D,E分別為AC,AB的中點,點F為線段CD上的一點,將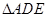 沿DE折起到
沿DE折起到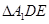 的位置,使
的位置,使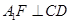 ,如圖2.
,如圖2.
(Ⅰ)求證:DE∥平面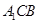
(Ⅱ)求證: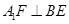
(Ⅲ)線段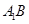 上是否存在點Q,使
上是否存在點Q,使 ?說明理由。
?說明理由。
【解析】(1)∵DE∥BC,由線面平行的判定定理得出
(2)可以先證 ,得出
,得出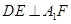 ,∵
,∵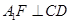 ∴
∴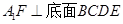
∴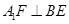
(3)Q為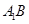 的中點,由上問
的中點,由上問 ,易知
,易知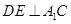 ,取
,取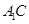 中點P,連接DP和QP,不難證出
中點P,連接DP和QP,不難證出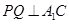 ,
,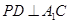 ∴
∴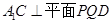 ∴
∴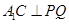 ,又∵
,又∵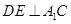 ∴
∴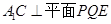
已知 .
.
(1)求 的單調區間;
的單調區間;
(2)證明:當 時,
時, 恒成立;
恒成立;
(3)任取兩個不相等的正數 ,且
,且 ,若存在
,若存在 使
使 成立,證明:
成立,證明: .
.
【解析】(1)g(x)=lnx+ ,
, =
=
 (1’)
(1’)
當k 0時,
0時, >0,所以函數g(x)的增區間為(0,+
>0,所以函數g(x)的增區間為(0,+ ),無減區間;
),無減區間;
當k>0時, >0,得x>k;
>0,得x>k; <0,得0<x<k∴增區間(k,+
<0,得0<x<k∴增區間(k,+ )減區間為(0,k)(3’)
)減區間為(0,k)(3’)
(2)設h(x)=xlnx-2x+e(x 1)令
1)令 = lnx-1=0得x=e, 當x變化時,h(x),
= lnx-1=0得x=e, 當x變化時,h(x), 的變化情況如表
的變化情況如表
|
x |
1 |
(1,e) |
e |
(e,+ |
|
|
|
- |
0 |
+ |
|
h(x) |
e-2 |
|
0 |
↗ |
所以h(x) 0, ∴f(x)
0, ∴f(x) 2x-e
(5’)
2x-e
(5’)
設G(x)=lnx- (x
(x 1)
1)  =
= =
=
 0,當且僅當x=1時,
0,當且僅當x=1時, =0所以G(x) 為減函數, 所以G(x)
=0所以G(x) 為減函數, 所以G(x)  G(1)=0, 所以lnx-
G(1)=0, 所以lnx-
 0所以xlnx
0所以xlnx
 (x
(x 1)成立,所以f(x)
1)成立,所以f(x) 
 ,綜上,當x
,綜上,當x 1時, 2x-e
1時, 2x-e f(x)
f(x)
 恒成立.
恒成立.
(3) ∵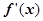 =lnx+1∴lnx0+1=
=lnx+1∴lnx0+1= =
= ∴lnx0=
∴lnx0=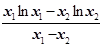 -1
∴lnx0 –lnx
-1
∴lnx0 –lnx =
= -1–lnx
-1–lnx =
= =
= =
= (10’) 設H(t)=lnt+1-t(0<t<1),
(10’) 設H(t)=lnt+1-t(0<t<1),
 =
= =
=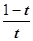 >0(0<t<1), 所以H(t) 在(0,1)上是增函數,并且H(t)在t=1處有意義, 所以H(t)
<H(1)=0∵
>0(0<t<1), 所以H(t) 在(0,1)上是增函數,并且H(t)在t=1處有意義, 所以H(t)
<H(1)=0∵ ∴
∴ =
=
∴lnx0 –lnx >0, ∴x0 >x
>0, ∴x0 >x
已知 ,(其中
,(其中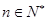 )
)
⑴求 及
及 ;
;
⑵試比較 與
與 的大小,并說明理由.
的大小,并說明理由.
【解析】第一問中取 ,則
,則 ;
…………1分
;
…………1分
對等式兩邊求導,得
取 ,則
,則 得到結論
得到結論
第二問中,要比較 與
與 的大小,即比較:
的大小,即比較: 與
與 的大小,歸納猜想可得結論當
的大小,歸納猜想可得結論當 時,
時, ;
;
當 時,
時, ;
;
當 時,
時, ;
;
猜想:當 時,
時, 運用數學歸納法證明即可。
運用數學歸納法證明即可。
解:⑴取 ,則
,則 ;
…………1分
;
…………1分
對等式兩邊求導,得 ,
,
取 ,則
,則 。 …………4分
。 …………4分
⑵要比較 與
與 的大小,即比較:
的大小,即比較: 與
與 的大小,
的大小,
當 時,
時, ;
;
當 時,
時, ;
;
當 時,
時, ;
…………6分
;
…………6分
猜想:當 時,
時, ,下面用數學歸納法證明:
,下面用數學歸納法證明:
由上述過程可知, 時結論成立,
時結論成立,
假設當 時結論成立,即
時結論成立,即 ,
,
當 時,
時,
而
∴
即 時結論也成立,
時結論也成立,
∴當 時,
時, 成立。
…………11分
成立。
…………11分
綜上得,當 時,
時, ;
;
當 時,
時, ;
;
當 時,
時,
某校從參加高三年級理科綜合物理考試的學生中隨機抽出 名學生,將其數學成績(均為整數)分成六段
名學生,將其數學成績(均為整數)分成六段 ,
, …
… 后得到如下部分頻率分布直方圖.觀察圖形的信息,回答下列問題:
后得到如下部分頻率分布直方圖.觀察圖形的信息,回答下列問題:
(Ⅰ)求分數在 內的頻率,并補全這個頻率分布直方圖;
內的頻率,并補全這個頻率分布直方圖;
(Ⅱ)統計方法中,同一組數據常用該組區間的中點值作為代表,據此估計本次考試的
平均分;
(Ⅲ)若從 名學生中隨機抽取
名學生中隨機抽取 人,抽到的學生成績在
人,抽到的學生成績在 記
記 分,在
分,在 記
記 分,
分,
在 記
記 分,用
分,用 表示抽取結束后的總記分,求
表示抽取結束后的總記分,求 的分布列和數學期望.
的分布列和數學期望.

【解析】(1)中利用直方圖中面積和為1,可以求解得到分數在 內的頻率為
內的頻率為
(2)中結合平均值可以得到平均分為:
(3)中用 表示抽取結束后的總記分x, 學生成績在
表示抽取結束后的總記分x, 學生成績在 的有
的有 人,在
人,在 的有
的有 人,在
人,在 的有
的有 人,結合古典概型的概率公式求解得到。
人,結合古典概型的概率公式求解得到。
(Ⅰ)設分數在 內的頻率為
內的頻率為 ,根據頻率分布直方圖,則有
,根據頻率分布直方圖,則有 ,可得
,可得 ,所以頻率分布直方圖如右圖.……4分
,所以頻率分布直方圖如右圖.……4分


(求解頻率3分,畫圖1分)
(Ⅱ)平均分為: ……7分
……7分
(Ⅲ)學生成績在 的有
的有 人,在
人,在 的有
的有 人,
人,
在 的有
的有 人.并且
人.并且 的可能取值是
的可能取值是 . ………8分
. ………8分
則 ;
; ;
;
 ;
;
 ;
; .(每個1分)
.(每個1分)
所以 的分布列為
的分布列為
|
|
0 |
1 |
2 |
3 |
4 |
|
|
|
|
|
|
|
…………………13分

已知函數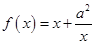 ,
,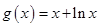 ,其中
,其中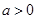 .
.
(1)若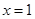 是函數
是函數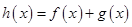 的極值點,求實數
的極值點,求實數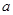 的值;
的值;
(2)若對任意的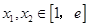 (
(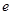 為自然對數的底數)都有
為自然對數的底數)都有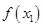 ≥
≥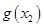 成立,求實數
成立,求實數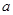 的取值范圍.
的取值范圍.
【解析】(1)根據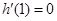 建立關于a的方程求a即可.
建立關于a的方程求a即可.
(2)本題要分別求出f(x)在[1,e]上的最小值,g(x)在[1,e]上的最大值,然后
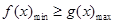 ,解關于a的不等式即可.
,解關于a的不等式即可.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com