
題目列表(包括答案和解析)
(本小題滿分12分)
已知直線 過拋物線
過拋物線 的焦點
的焦點 且與拋物線相交于兩點
且與拋物線相交于兩點 ,自
,自 向準線
向準線 作垂線,垂足分別為
作垂線,垂足分別為 .
.
(Ⅰ)求拋物線 的方程;
的方程;
(Ⅱ)證明:無論 取何實數(shù)時,
取何實數(shù)時, ,
, 都是定值;
都是定值;
 (III)記
(III)記 的面積分別為
的面積分別為 ,試判斷
,試判斷 是否成立,并證明你的結(jié)論.
是否成立,并證明你的結(jié)論.
(本小題滿分12分)
已知直線![]() 過拋物線
過拋物線![]() 的焦點
的焦點![]() 且與拋物線相交于兩點
且與拋物線相交于兩點![]() ,自
,自![]() 向準線
向準線![]() 作垂線,垂足分別為
作垂線,垂足分別為![]() .
.
(Ⅰ)求拋物線![]() 的方程;
的方程;
(Ⅱ)證明:無論![]() 取何實數(shù)時,
取何實數(shù)時,![]() ,
,![]() 都是定值;
都是定值;
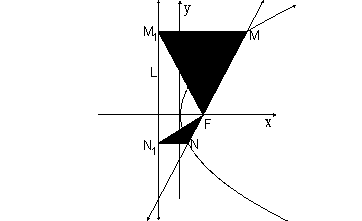 (III)記
(III)記![]() 的面積分別為
的面積分別為![]() ,試判斷
,試判斷![]() 是否成立,并證明你的結(jié)論.
是否成立,并證明你的結(jié)論.
(2012福建理)受轎車在保修期內(nèi)維修費等因素的影響,企業(yè)生產(chǎn)每輛轎車的利潤與該轎車首次出現(xiàn)故障的時間有關,某轎車制造廠生產(chǎn)甲、乙兩種品牌轎車,保修期均為2年,現(xiàn)從該廠已售出的兩種品牌轎車中隨機抽取50輛,統(tǒng)計書數(shù)據(jù)如下:
| 品牌 | 甲 | 乙 | |||
| 首次出現(xiàn)故障時間 |
|
|
|
|
|
| 轎車數(shù)量(輛) | 2 | 3 | 45 | 5 | 45 |
| 輛利潤(萬元) | 1 | 2 | 3 |
|
|
將頻率視為概率,解答下列問題:
(I)從該廠生產(chǎn)的甲品牌轎車中隨機抽取一輛,求首次出現(xiàn)故障發(fā)生在保修期內(nèi)的概率;
(II)若該廠生產(chǎn)的轎車均能售出,記住生產(chǎn)一輛甲品牌轎車的利潤為![]() ,生產(chǎn)一輛乙品牌轎車的利潤為
,生產(chǎn)一輛乙品牌轎車的利潤為![]() ,分別求
,分別求![]() 的分布列;
的分布列;
(III)該廠預計今后這兩種品牌轎車銷量相當,由于資金限制,只能生產(chǎn)其中一種品牌轎車,若從經(jīng)濟效益的角度考慮,你認為應該產(chǎn)生哪種品牌的轎車?說明理由.
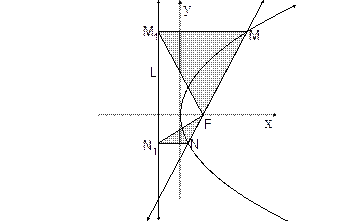
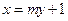 過拋物線
過拋物線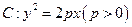 的焦點
的焦點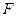 且與拋物線相交于兩點
且與拋物線相交于兩點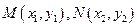 ,自
,自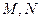 向準線
向準線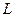
 作垂線,垂足分別為
作垂線,垂足分別為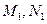 .
.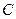 的方程;
的方程;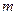 取何實數(shù)時,
取何實數(shù)時,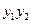 ,
,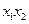 都是定值;
都是定值;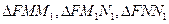 的面積分別為
的面積分別為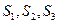 ,試判斷
,試判斷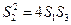 是否成立,并證明你的結(jié)論.
是否成立,并證明你的結(jié)論.(04年全國卷III文)記函數(shù)![]() 的反函數(shù)為
的反函數(shù)為![]() ,則
,則![]() ( )
( )
A. 2 B. ![]() C. 3 D.
C. 3 D. ![]()
一、選擇題:本大題共12小題,每小題5分,共60分。
1―6AABCBD 7―12ACDCBD
二、填空題:本大題共4小題,每小題5分,共20分。
13.60° 14.-8 15.量檢測%20數(shù)學理科.files/image125.gif) 16.6
16.6
三、解答題:本大題共6小題,共70分,解答應寫出文字說明,證明過程或演算步驟。
17.(本小題滿分10分)
(I)解:因為量檢測%20數(shù)學理科.files/image127.gif)
由正弦定理得量檢測%20數(shù)學理科.files/image129.gif)
所以量檢測%20數(shù)學理科.files/image131.gif)
又量檢測%20數(shù)學理科.files/image133.gif)
故量檢測%20數(shù)學理科.files/image135.gif) 5分
5分
(II)由量檢測%20數(shù)學理科.files/image137.gif)
故量檢測%20數(shù)學理科.files/image139.gif)
量檢測%20數(shù)學理科.files/image141.gif) 10分
10分
18.(本小題滿分12分)
(I)解:當量檢測%20數(shù)學理科.files/image143.gif)
故量檢測%20數(shù)學理科.files/image145.gif) 1分
1分
因為 當量檢測%20數(shù)學理科.files/image147.gif)
當量檢測%20數(shù)學理科.files/image149.gif)
故量檢測%20數(shù)學理科.files/image151.gif) 上單調(diào)遞減。
5分
上單調(diào)遞減。
5分
(II)解:由題意知量檢測%20數(shù)學理科.files/image153.gif) 上恒成立,
上恒成立,
即量檢測%20數(shù)學理科.files/image155.gif) 上恒成立。
7分
上恒成立。
7分
令量檢測%20數(shù)學理科.files/image157.gif)
因為量檢測%20數(shù)學理科.files/image159.gif) 9分
9分
故量檢測%20數(shù)學理科.files/image155.gif) 上恒成立等價于
上恒成立等價于
量檢測%20數(shù)學理科.files/image162.gif) 11分
11分
解得量檢測%20數(shù)學理科.files/image164.gif) 12分
12分
19.(本小題滿分12分)
(I)證明:量檢測%20數(shù)學理科.files/image166.gif)
量檢測%20數(shù)學理科.files/image168.gif) 2分
2分
又量檢測%20數(shù)學理科.files/image170.gif)