題目列表(包括答案和解析)
| S(k+1)n |
| Skn |
| 4 |
| 3 |
| 2 |
| 3 |
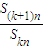是與n無關的非零常數t=f（k），則稱該數列{an}是“k類和科比數列”．
，求數列{an}的通項公式；
，求證數列cn是一個“1 類和科比數列”（4分）；數列{an}的前n項和記為Sn，前kn項和記為
Skn(n，k∈N*)，對給定的常數k，若
是與n無關的非零常數t＝f(k)，則稱該數列{an}是“k類和科比數列”，
(1)已知Sn＝
an－
(n∈N*)，求數列{an}的通項公式；
(2)在(1)的條件下，數列an＝2cn，求證數列{cn}是一個“1類和科比數列”；
(3)、設等差數列{bn}是一個“k類和科比數列”，其中首項b1，公差D，探究b1
與D的數量關系，并寫出相應的常數t＝f(k)；
| 1 | 2 |
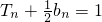．一、選擇題：本大題共10個小題，每小題5分，共50分．
題號
1
2
3
4
5
6
7
8
9
10
答案
C
B
C
D
C
B
A
D
B
A
二、填空題：本大題共4個小題，每小題4分，共16分．
11. 630 12. 2k 13. 
14. ①②③
三、解答題：本大題共6個小題，每小題14分，共84分．
15．
(4分) 
由題意得
16． 
有分布列：
0
1
2
3
P
從而期望
17．（1）
又
(2) 
(3)DE//AB,
(4)設BB1的中點為F，連接EF、DF，則EF是DF在平面BB
因為BB
18.(1) 由題意得
(2) 
所以直線
的斜率為
令
，則直線的斜率
，
19．（1）由韋達定理得
是首項為4，公差為2的等差數列。
（2）由（1）知
，則
原式左邊=
=
=右式。故原式成立。
20．令x=y=0，有
，令y=-x則
得
故（1）得證。
（2）在R上任取x1,x2且
，且
，
所以
在R上單調遞增；
（3）
由
得
；
由
得
；因為
，
所以
無解，即圓心到直線的距離大于或等于半徑2，只需
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com