
【題目】如圖所示, ![]() 是某海灣旅游區(qū)的一角,為營造更加優(yōu)美的旅游環(huán)境,旅游區(qū)管委會決定建立面積為
是某海灣旅游區(qū)的一角,為營造更加優(yōu)美的旅游環(huán)境,旅游區(qū)管委會決定建立面積為![]() 平分千米的三角形主題游戲樂園
平分千米的三角形主題游戲樂園![]() ,并在區(qū)域
,并在區(qū)域![]() 建立水上餐廳.
建立水上餐廳.
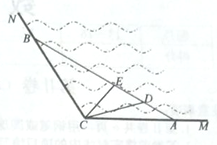
已知![]() ,
, ![]() .
.
(1)設![]() ,
, ![]() ,用
,用![]() 表示
表示![]() ,并求
,并求![]() 的最小值;
的最小值;
(2)設![]() (
(![]() 為銳角),當
為銳角),當![]() 最小時,用
最小時,用![]() 表示區(qū)域
表示區(qū)域![]() 的面積
的面積![]() ,并求
,并求![]() 的最小值.
的最小值.
【答案】(1) ![]() ;(2)S=
;(2)S=![]() ,8-
,8-![]() .
.
【解析】試題分析:
(1)首先確定函數(shù)的解析式為![]() 結合均值不等式的結論可得
結合均值不等式的結論可得![]() 的最小值是
的最小值是![]() ;
;
(2)結合題意和三角函數(shù)的性質可得S=![]() ,利用三角函數(shù)的性質可知
,利用三角函數(shù)的性質可知![]() 的最小值是8-
的最小值是8-![]() .
.
試題解析:
(1)由S△ACB=![]() AC·BC·sin∠ACB=4
AC·BC·sin∠ACB=4![]() 得,BC=
得,BC=![]() ,
,
在△ACB中,由余弦定理可得,AB2=AC2+BC2-2AC·BC·cos∠ACB,
即y2=x 2+![]() +16,
+16,
所以y=![]()
y=![]() ≥
≥![]() =4
=4![]() ,
,
當且僅當x2=![]() ,即x=4時取等號.
,即x=4時取等號.
所以當x=4時,y有最小值4![]() .
.
(2)由(1)可知,AB=4![]() ,AC=BC=4,所以∠BAC=30°,
,AC=BC=4,所以∠BAC=30°,
在△ACD中,由正弦定理,CD=![]() =
=![]() =
=![]() ,
,
在△ACE中,由正弦定理,CE=![]() =
=![]() =
=![]() ,
,
所以,S=![]() CD·CE·sin∠DCE=
CD·CE·sin∠DCE=![]() =
=![]() .
.
因為θ為銳角,
所以當θ=![]() 時,S有最小值8-4
時,S有最小值8-4![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() (
(![]() ).
).
(1)若函數(shù)![]() 有零點,求實數(shù)
有零點,求實數(shù)![]() 的取值范圍;
的取值范圍;
(2)若對任意的![]() ,都有
,都有![]() ,求實數(shù)
,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】【選修4-4:坐標系與參數(shù)方程】
已知圓![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)).若直線
為參數(shù)).若直線![]() 與圓
與圓![]() 相交于不同的兩點
相交于不同的兩點![]() .
.
(1)寫出圓![]() 的直角坐標方程,并求圓心的坐標與半徑;
的直角坐標方程,并求圓心的坐標與半徑;
(2)若弦長![]() ,求直線
,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() .
.
(1)若函數(shù)![]() 有且只有一個極值點,求實數(shù)
有且只有一個極值點,求實數(shù)![]() 的取值范圍;
的取值范圍;
(2)對于函數(shù)![]() ,
,![]() ,
,![]() ,若對于區(qū)間
,若對于區(qū)間![]() 上的任意一個
上的任意一個![]() ,都有
,都有![]() ,則稱函數(shù)
,則稱函數(shù)![]() 是函數(shù)
是函數(shù)![]() ,
,![]() 在區(qū)間
在區(qū)間![]() 上的一個“分界函數(shù)”.已知
上的一個“分界函數(shù)”.已知![]() ,
,![]() ,問是否存在實數(shù)
,問是否存在實數(shù)![]() ,使得函數(shù)
,使得函數(shù)![]() 是函數(shù)
是函數(shù)![]() ,
,![]() 在區(qū)間
在區(qū)間![]() 上的一個“分界函數(shù)”?若存在,求實數(shù)
上的一個“分界函數(shù)”?若存在,求實數(shù)![]() 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設函數(shù)![]() ,其中
,其中![]() ,若
,若![]() 是
是![]() 的三條邊長,則下列結論中正確的是( )
的三條邊長,則下列結論中正確的是( )
①存在![]() ,使
,使![]() 、
、![]() 、
、![]() 不能構成一個三角形的三條邊
不能構成一個三角形的三條邊
②對一切![]() ,都有
,都有![]()
③若![]() 為鈍角三角形,則存在
為鈍角三角形,則存在![]() ,使
,使![]()
A. ①② B. ①③ C. ②③ D. ①②③
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】4個男生,3個女生站成一排.(必須寫出算式再算出結果才得分)
(Ⅰ)3個女生必須排在一起,有多少種不同的排法?
(Ⅱ)任何兩個女生彼此不相鄰,有多少種不同的排法?
(Ⅲ)甲乙二人之間恰好有三個人,有多少種不同的排法?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】長為![]() 的線段
的線段![]() 的兩個端點
的兩個端點![]() 和
和![]() 分別在
分別在![]() 軸和
軸和![]() 軸上滑動.
軸上滑動.
(1)求線段![]() 的中點的軌跡
的中點的軌跡![]() 的方程;
的方程;
(2)當![]() 時,曲線
時,曲線![]() 與
與![]() 軸交于
軸交于![]() 兩點,點
兩點,點![]() 在線段
在線段![]() 上,過
上,過![]() 作
作![]() 軸的垂線交曲線
軸的垂線交曲線![]() 于不同的兩點
于不同的兩點![]() ,點
,點![]() 在線段
在線段![]() 上,滿足
上,滿足![]() 與
與![]() 的斜率之積為-2,試求
的斜率之積為-2,試求![]() 與
與![]() 的面積之比.
的面積之比.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某校對高二年段的男生進行體檢,現(xiàn)將高二男生的體重![]() 數(shù)據(jù)進行整理后分成6組,并繪制部分頻率分布直方圖(如圖所示).已知第三組
數(shù)據(jù)進行整理后分成6組,并繪制部分頻率分布直方圖(如圖所示).已知第三組![]() 的人數(shù)為200.根據(jù)一般標準,高二男生體重超過
的人數(shù)為200.根據(jù)一般標準,高二男生體重超過![]() 屬于偏胖,低于
屬于偏胖,低于![]() 屬于偏瘦.觀察圖形的信息,回答下列問題:
屬于偏瘦.觀察圖形的信息,回答下列問題:
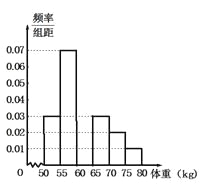
(1)求體重在![]() 內的頻率,并補全頻率分布直方圖;
內的頻率,并補全頻率分布直方圖;
(2)用分層抽樣的方法從偏胖的學生中抽取![]() 人對日常生活習慣及體育鍛煉進行調查,則各組應分別抽取多少人?
人對日常生活習慣及體育鍛煉進行調查,則各組應分別抽取多少人?
(3)根據(jù)頻率分布直方圖,估計高二男生的體重的中位數(shù)與平均數(shù).
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com