Question

為了解某班學生關注NBA是否與性別有關，對本班48人進行了問卷調查得到如下的列聯表：

	關注NBA	不關注NBA	合  計
男   生		6
女   生	10
合   計			48

 
已知在全班48人中隨機抽取1人，抽到關注NBA的學生的概率為2/3
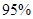⑴請將上面列連表補充完整，并判斷是否有的把握認為關注NBA與性別有關？
⑵現從女生中抽取2人進一步調查，設其中關注NBA的女生人數為X，求X的分布列與數學期望.
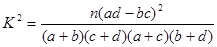附：，其中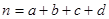

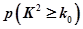	0.15	0.10	0.05	0.025	0.010
	2.072	2.706	3.841	5.024	6.635

 

Answer 1

(1)關注NBA與性別有關；（2）分布列（略），E（X）=1.

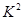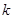解析試題分析：（1）本小題獨立性檢測的應用，本小題的關鍵是計算出的觀測值,和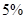對應的臨界值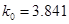，根據關注NBA的學生的概率為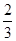，可知關注NBA的學生為32（估計值）.根據條件填滿表格，然后計算出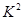，并判斷其與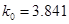的大小關系，得出結論.（2）對于分布列問題：首先應弄清隨機變量是誰以及隨機變量的取值范圍，然后就是每個隨機變量下概率的取值，最后列表計算期望.
試題解析：
(1）將列聯表補充完整有：

	關注NBA	不關注NBA	合 計
男生	22	6	28
女生	10	10	20
合計	32	16	48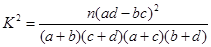

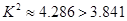由,計算可得                  4分
因此，在犯錯的概率不超過0.05的前提下認為學生關注NBA與性別有關，
即有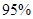把握認為關注NBA與性別有關                                          6分
（2）由題意可知，X的取值為0，1，2，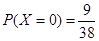
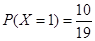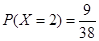,,                                 9分
所以X的分布列為

<abbr id="qnirv"><strong id="qnirv"></strong></abbr>

<td id="qnirv"><rp id="qnirv"><video id="qnirv"></video></rp></td>

<tt id="qnirv"><em id="qnirv"></em></tt>

X	0	1	2
p