
【題目】如圖,![]() 、
、![]() 分別為橢圓
分別為橢圓![]() 的焦點,橢圓的右準線
的焦點,橢圓的右準線![]() 與
與![]() 軸交于
軸交于![]() 點,若
點,若![]() ,且
,且![]() .
.

(Ⅰ)求橢圓的方程;
(Ⅱ)過![]() 、
、![]() 作互相垂直的兩直線分別與橢圓交于
作互相垂直的兩直線分別與橢圓交于![]() 、
、![]() 、
、![]() 、
、![]() 四點,求四邊形
四點,求四邊形![]() 面積的取值范圍.
面積的取值范圍.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
(I) 先確定A點坐標為(a2,0),利用![]() ,可得F2是AF1的中點,由此可求橢圓方程;(II)當直線MN與PQ中有一條與x軸垂直時,四邊形PMQN面積
,可得F2是AF1的中點,由此可求橢圓方程;(II)當直線MN與PQ中有一條與x軸垂直時,四邊形PMQN面積![]() ;當直線PQ,MN均與x軸不垂直時,設直線PQ、MN的方程與橢圓方程聯立,求得|PQ|,|MN|,表示出四邊形PMQN面積,再換元,即可求得四邊形PMQN面積的取值范圍.
;當直線PQ,MN均與x軸不垂直時,設直線PQ、MN的方程與橢圓方程聯立,求得|PQ|,|MN|,表示出四邊形PMQN面積,再換元,即可求得四邊形PMQN面積的取值范圍.
(Ⅰ)由![]() 得
得![]() ,∴
,∴![]() 點坐標為
點坐標為![]() ;∵
;∵![]() ∴
∴![]() 是
是![]() 的中點∴
的中點∴![]() ,
,![]() ∴橢圓方程為
∴橢圓方程為![]()
(Ⅱ)當直線![]() 與
與![]() 之一與
之一與![]() 軸垂直時,四邊形
軸垂直時,四邊形![]() 面積
面積![]() ;
;
當直線![]() ,
,![]() 均與
均與![]() 軸不垂直時,不妨設
軸不垂直時,不妨設![]() ,
,
聯立 代入消去
代入消去![]() 得
得![]()
設![]() ,
,![]() 則
則![]() ,
,![]()
∴![]() ,同理
,同理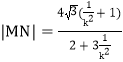
∴四邊形![]() 面積
面積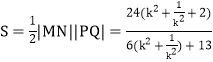
令![]() ,則
,則![]() ,
,![]() ,易知
,易知![]() 是以
是以![]() 為變量的增函數
為變量的增函數
所以當![]() ,
,![]() 時,
時,![]() ,∴
,∴![]()
綜上可知,![]() ,∴四邊形
,∴四邊形![]() 面積的取值范圍為
面積的取值范圍為![]()


 千里馬走向假期期末仿真試卷寒假系列答案
千里馬走向假期期末仿真試卷寒假系列答案科目:高中數學 來源: 題型:
【題目】在極坐標系中,直線l的極坐標方程為ρcosθ=4,曲線C的極坐標方程為ρ=2cosθ+2sinθ,以極點為坐標原點O,極軸為x軸的正半軸建立直角坐標系,射線l':y=kx(x≥0,0<k<1)與曲線C交于O,M兩點.
(Ⅰ)寫出直線l的直角坐標方程以及曲線C的參數方程;
(Ⅱ)若射線l′與直線l交于點N,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2016高考新課標II,理15)有三張卡片,分別寫有1和2,1和3,2和3.甲,乙,丙三人各取走一張卡片,甲看了乙的卡片后說:“我與乙的卡片上相同的數字不是2”,乙看了丙的卡片后說:“我與丙的卡片上相同的數字不是1”,丙說:“我的卡片上的數字之和不是5”,則甲的卡片上的數字是________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為維護交通秩序,防范電動自行車被盜,天津市公安局決定,開展二輪電動自行車免費登記、上牌照工作.電動自行車牌照分免費和收費(安裝防盜裝置)兩大類,群眾可以 自愿選擇安裝.已知甲、乙、丙三個不同類型小區的人數分別為15000,15000,20000.交管部門為了解社區居民意愿,現采用分層抽樣的方法從中抽取10人進行電話訪談.
(Ⅰ)應從甲小區和丙小區的居民中分別抽取多少人?
(Ⅱ)設從甲小區抽取的居民為![]() ,丙小區抽取的居民為
,丙小區抽取的居民為![]() .現從甲小區和丙小區已抽取的居民中隨機抽取2人接受問卷調查.
.現從甲小區和丙小區已抽取的居民中隨機抽取2人接受問卷調查.
(ⅰ)試用所給字母列舉出所有可能的抽取結果;
(ⅱ)設![]() 為事件“抽取的2人來自不同的小區”,求事件
為事件“抽取的2人來自不同的小區”,求事件![]() 發生的概率.
發生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了引導居民合理用電,國家決定實行合理的階梯電價,居民用電原則上以住宅為單位(一套住宅為一戶).

某市隨機抽取10戶同一個月的用電情況,得到統計表如下:

(1)若規定第一階梯電價每度0.5元,第二階梯超出第一階梯的部分每度0.6元,第三階梯超出第二階梯每度0.8元,試計算![]() 居民用電戶用電410度時應交電費多少元?
居民用電戶用電410度時應交電費多少元?
(2)現要在這10戶家庭中任意選取3戶,求取到第二階梯電量的戶數的分布列與期望;
(3)以表中抽到的10戶作為樣本估計全市居民用電,現從全市中依次抽取10戶,若抽到![]() 戶用電量為第一階梯的可能性最大,求
戶用電量為第一階梯的可能性最大,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】每年五月最受七中學子期待的學生活動莫過于學生節,在每屆學生節活動中,著七中校服的布偶“七中熊”尤其受同學和老師歡迎.已知學生會將在學生節當天售賣“七中熊”,并且會將所獲得利潤全部捐獻于公益組織.為了讓更多同學知曉,學生會宣傳部需要前期在學校張貼海報宣傳,成本為250元,并且當學生會向廠家訂制![]() 只“七中熊”時,需另投入成本
只“七中熊”時,需另投入成本![]() ,
,![]() (元),
(元),![]() .通過市場分析, 學生會訂制的“七中熊”能全部售完.若學生節當天,每只“七中熊”售價為70元,則當銷量為______只時,學生會向公益組織所捐獻的金額會最大.
.通過市場分析, 學生會訂制的“七中熊”能全部售完.若學生節當天,每只“七中熊”售價為70元,則當銷量為______只時,學生會向公益組織所捐獻的金額會最大.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com