
【題目】已知f ( x)= ![]() x2 , g ( x)=a ln x(a>0).
x2 , g ( x)=a ln x(a>0).
(Ⅰ)求函數 F ( x)=f(x)g(x)的極值
(Ⅱ)若函數 G( x)=f(x)﹣g(x)+(a﹣1)在區間 ( ![]() ,e) 內有兩個零點,求的取值范圍;
,e) 內有兩個零點,求的取值范圍;
(Ⅲ)函數 h( x)=g ( x )﹣x+ ![]() ,設 x1∈(0,1),x2∈(1,+∞),若 h( x 2)﹣h( x 1)存在最大值,記為 M (a),則當 a≤e+1
,設 x1∈(0,1),x2∈(1,+∞),若 h( x 2)﹣h( x 1)存在最大值,記為 M (a),則當 a≤e+1 ![]() 時,M (a) 是否存在最大值?若存在,求出其最大值;若不存在,請說明理由.
時,M (a) 是否存在最大值?若存在,求出其最大值;若不存在,請說明理由.
【答案】解:(Ⅰ) ![]() , ∴
, ∴ ![]() ,
,
由F′(x)>0得 ![]() ,
,
由F′(x)<0,得 ![]()
∴F(x)在 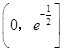 上單調遞減,在
上單調遞減,在 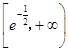 上單調遞增,
上單調遞增,
∴ 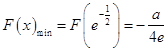 ,F(x)無極大值.
,F(x)無極大值.
(Ⅱ) ![]()
∴ ![]()
又 ![]() ,易得G(x)在
,易得G(x)在 ![]() 上單調遞減,在[1,e)上單調遞增,
上單調遞減,在[1,e)上單調遞增,
要使函數G(x)在 ![]() 內有兩個零點,
內有兩個零點,
需 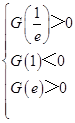 ,即
,即 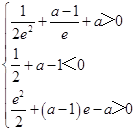 ,
,
∴ 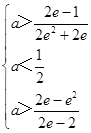 ,
,
∴ ![]() ,即a的取值范圍是
,即a的取值范圍是 ![]() .
.
(Ⅲ)若0<a≤2,∵ ![]() 在(0,+∞)上滿足h′(x)≤0,
在(0,+∞)上滿足h′(x)≤0,
∴h(x)在(0,+∞)上單調遞減,∴h(x2)﹣h(x1)<0.
∴h(x2)﹣h(x1)不存在最大值,則a>2,
∴方程x2﹣ax+1=0有兩個不相等的正實數根,
令其為m,n,且不妨設0<m<1<n,則 ![]() ,
,
h(x)在(0,m)上單調遞減,在(m,n)上調遞增,在(n,+∞)上單調遞減,
對x1∈(0,1),有h(x1)≥h(m);對x2∈(1,+∞),有h(x2)≤h(n),
∴[h(x2)﹣h(x1)]max=h(n)﹣h(m).
∴ ![]() =
= ![]() .
.
將 ![]() ,
, ![]() 代入上式,消去a,m,
代入上式,消去a,m,
得: ![]() ,
,
∵ ![]() ,∴
,∴ ![]() ,n>1.
,n>1.
據 ![]() 在x∈(1,+∞)上單調遞增,得n∈(1,e],
在x∈(1,+∞)上單調遞增,得n∈(1,e],
設 ![]() ,x∈(1,e],
,x∈(1,e],![]() ,x∈(1,e],
,x∈(1,e],
∴φ′(x)>0,即φ(x)在(1,e]上單調遞增,
∴ ![]() ,
,
∴M(a)存在最大值為 ![]()
【解析】(Ⅰ)求出函數的導數,解關于導函數的不等式,求出函數的單調區間即可;(Ⅱ)求出函數的導數,根據函數的單調性得到關于a的不等式組,解出即可;(Ⅲ)求出函數的導數,得到方程x2﹣ax+1=0有兩個不相等的正實數根,令其為m,n,根據函數的單調性判斷即可.
【考點精析】認真審題,首先需要了解函數的極值與導數(求函數![]() 的極值的方法是:(1)如果在
的極值的方法是:(1)如果在![]() 附近的左側
附近的左側![]() ,右側
,右側![]() ,那么
,那么![]() 是極大值(2)如果在
是極大值(2)如果在![]() 附近的左側
附近的左側![]() ,右側
,右側![]() ,那么
,那么![]() 是極小值),還要掌握函數的最大(小)值與導數(求函數
是極小值),還要掌握函數的最大(小)值與導數(求函數![]() 在
在![]() 上的最大值與最小值的步驟:(1)求函數
上的最大值與最小值的步驟:(1)求函數![]() 在
在![]() 內的極值;(2)將函數
內的極值;(2)將函數![]() 的各極值與端點處的函數值
的各極值與端點處的函數值![]() ,
,![]() 比較,其中最大的是一個最大值,最小的是最小值)的相關知識才是答題的關鍵.
比較,其中最大的是一個最大值,最小的是最小值)的相關知識才是答題的關鍵.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】4月23日是世界讀書日,惠州市某中學在此期間開展了一系列的讀書教育活動。為了解本校學生課外閱讀情況,學校隨機抽取了100名學生對其課外閱讀時間進行調查。下面是根據調查結果繪制的學生日均課外閱讀時間(單位:分鐘)的頻率分布直方圖,且將日均課外閱讀時間不低于60分鐘的學生稱為“讀書迷”,低于60分鐘的學生稱為“非讀書迷”.
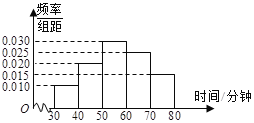
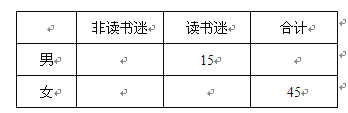
(Ⅰ)根據已知條件完成下面2×2列聯表,并據此判斷是否有99%的把握認為“讀書迷”與性別有關?
(Ⅱ)將頻率視為概率,現在從該校大量學生中用隨機抽樣的方法每次抽取1人,共抽取3次,記被抽取的3人中“讀書迷”的人數為![]() ,若每次抽取的結果是相互獨立的,求
,若每次抽取的結果是相互獨立的,求![]() 的分布列、數學期望
的分布列、數學期望![]() 和方差
和方差![]() .
.
附: 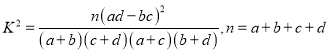
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() (a>b>0 ) 經過點 P(1,
(a>b>0 ) 經過點 P(1, ![]() ),離心率 e=
),離心率 e= ![]()
(Ⅰ)求橢圓C的標準方程.
(Ⅱ)設過點E(0,﹣2 ) 的直線l 與C相交于P,Q兩點,求△OPQ 面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的圖象過原點,且在
的圖象過原點,且在![]() 處取得極值,直線
處取得極值,直線![]() 與曲線
與曲線![]() 在原點處的切線互相垂直.
在原點處的切線互相垂直.
(Ⅰ)求函數![]() 的解析式;
的解析式;
(Ⅱ)若對任意實數的![]() ,恒有
,恒有![]() 成立,求實數
成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《數學九章》中對已知三角形三邊長求三角形的面積的求法填補了我國傳統數學的一個空白,與著名的海倫公式完全等價,由此可以看出我國古代已具有很高的數學水平,其求法是:“以小斜冪并大斜冪減中斜冪,余半之,自乘于上.以小斜冪乘大斜冪減上,余四約之,為實.一為從隔,開平方得積.”若把以上這段文字寫成公式,即S= ![]() .現有周長為2
.現有周長為2 ![]() +
+ ![]() 的△ABC滿足sinA:sinB:sinC=(
的△ABC滿足sinA:sinB:sinC=( ![]() ﹣1):
﹣1): ![]() :(
:( ![]() +1),試用以上給出的公式求得△ABC的面積為( )
+1),試用以上給出的公式求得△ABC的面積為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了得到函數y=sin(2x﹣ ![]() )的圖象,可以將函數y=sin2x的圖象( )
)的圖象,可以將函數y=sin2x的圖象( )
A.向右平移 ![]() 個單位
個單位
B.向右平移 ![]() 個單位
個單位
C.向左平移 ![]() 個單位
個單位
D.向左平移 ![]() 個單位
個單位
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com