
【題目】已知函數![]() ,
,![]() ,且
,且![]() 與
與![]() 的圖象有一個斜率為1的公切線(
的圖象有一個斜率為1的公切線(![]() 為自然對數的底數).
為自然對數的底數).
(1)求![]() ;
;
(2)設函數![]() ,討論函數
,討論函數![]() 的零點個數.
的零點個數.
【答案】(1)![]() (2)見解析
(2)見解析
【解析】
(1)由![]() 與
與![]() 的圖象有一個斜率為1的公切線,分別對
的圖象有一個斜率為1的公切線,分別對![]() 與
與![]() 求導并求出切線方程,列出等量關系可得
求導并求出切線方程,列出等量關系可得![]() ;
;
(2)利用換元將![]() 轉化為二次函數,分類討論對其單調性,對圖像特點進行分析,分情況討論出函數
轉化為二次函數,分類討論對其單調性,對圖像特點進行分析,分情況討論出函數![]() 的零點個數.
的零點個數.
(1)![]() 可得
可得![]() .
.
![]() 在
在![]() 處的切線方程為
處的切線方程為![]() ,
,
即![]() .
.
![]()
![]() .
.
![]() 在
在![]() 處的切線方程為
處的切線方程為![]()
![]() ,
,
故![]()
可得![]() .
.
(2)由(1)可得![]() ,
,
![]() ,
,
令![]() ,則
,則![]() ,
,
![]() ,
,
![]() 時,
時,![]() 有兩根,
有兩根,
![]() 且
且![]() ,
,
![]() ,
,
得:![]() ,
,
在![]() 上,
上,![]() ,
,
在![]() 上,
上,![]() ,
,
此時,![]() .
.
又![]() 時,
時,![]() 時,
時,![]() .
.
故在![]() 和
和![]() 上,
上,
![]() 各有1個零點.
各有1個零點.
![]() 時,
時,![]()
![]() 最小值為
最小值為![]() ,故
,故![]() 僅有1個零點.
僅有1個零點.
![]() 時,
時,![]() .
.
其中![]() ,同
,同![]() ,
,
![]() 在
在![]() 與
與![]() 上,
上,
![]() 各有1個零點,
各有1個零點,
![]() 時,
時,![]() ,僅在
,僅在![]() 有1個零點,
有1個零點,
![]() 時,對方程
時,對方程![]() .
.
方程有兩個正根![]() ,
,![]() .
.
在![]() 上,
上,![]() ,在
,在![]() 上,
上,![]() ,在
,在![]() ,
,![]() .
.
由 ,可得
,可得![]() ,
,
故![]() .
.
![]()
![]()
![]() ,
,
故![]() .
.
故在![]() 上,
上,![]() ,
,
在![]() 上,
上,![]() ,
,
在![]() 上,
上,![]() 有1個零點:
有1個零點:![]() .
.
![]() 時,
時,![]() 恒成立,
恒成立,
![]() 為增函數,
為增函數,![]() 僅有1個零點:
僅有1個零點:![]() .
.
綜上,![]() 或
或![]() 時,
時,![]() 有1個零點,
有1個零點,
![]() 或
或![]() 時,
時,![]() 有2個零點.
有2個零點.


 雙基同步導航訓練系列答案
雙基同步導航訓練系列答案 黃岡小狀元同步計算天天練系列答案
黃岡小狀元同步計算天天練系列答案科目:高中數學 來源: 題型:
【題目】回收1噸廢紙可以生產出0.8噸再生紙,可能節約用水約100噸,節約用煤約1.2噸,回收1噸廢鉛蓄電池可再生鉛約0.6噸,可節約用煤約0.8噸,節約用水約120噸,回收每噸廢鉛蓄電池的費用約0.9萬元,回收1噸廢紙的費用約為0.2萬元.現用于回收廢紙和廢鉛蓄電池的費用不超過18萬元,在保證節約用煤不少于12噸的前提下,最多可節約用水約__________噸.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若橢圓![]() :
:![]() 與橢圓
與橢圓![]() :
:![]() 滿足
滿足![]() ,則稱這兩個橢圓相似,
,則稱這兩個橢圓相似,![]() 叫相似比.若橢圓
叫相似比.若橢圓![]() 與橢圓
與橢圓![]() 相似且過
相似且過![]() 點.
點.
(I)求橢圓![]() 的標準方程;
的標準方程;
(II)過點![]() 作斜率不為零的直線
作斜率不為零的直線![]() 與橢圓
與橢圓![]() 交于不同兩點
交于不同兩點![]() 、
、![]() ,
,![]() 為橢圓
為橢圓![]() 的右焦點,直線
的右焦點,直線![]() 、
、![]() 分別交橢圓
分別交橢圓![]() 于點
于點![]() 、
、![]() ,設
,設![]() ,
,![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市在創建國家級衛生城(簡稱“創衛”)的過程中,相關部門需了解市民對“創衛”工作的滿意程度,若市民滿意指數不低于0.8(注:滿意指數![]()
![]() ),“創衛”工作按原方案繼續實施,否則需進一步整改.為此該部門隨機調查了100位市民,根據這100位市民給“創衛”工作的滿意程度評分,按以下區間:
),“創衛”工作按原方案繼續實施,否則需進一步整改.為此該部門隨機調查了100位市民,根據這100位市民給“創衛”工作的滿意程度評分,按以下區間:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分為六組,得到如圖頻率分布直方圖:
分為六組,得到如圖頻率分布直方圖:
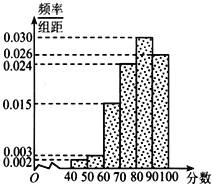
(1)為了解部分市民給“創衛”工作評分較低的原因,該部門從評分低于60分的市民中隨機選取2人進行座談,求這2人所給的評分恰好都在![]() 的概率;
的概率;
(2)根據你所學的統計知識,判斷該市“創衛”工作是否需要進一步整改,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若存在![]() ,使得
,使得![]() 對任意
對任意![]() 恒成立,則函數
恒成立,則函數![]() 在
在![]() 上有下界,其中
上有下界,其中![]() 為函數
為函數![]() 的一個下界;若存在
的一個下界;若存在![]() ,使得
,使得![]() 對任意
對任意![]() 恒成立,則函數
恒成立,則函數![]() 在
在![]() 上有上界,其中
上有上界,其中![]() 為函數
為函數![]() 的一個上界.如果一個函數既有上界又有下界,那么稱該函數有界.下列四個結論:
的一個上界.如果一個函數既有上界又有下界,那么稱該函數有界.下列四個結論:
①1不是函數![]() 的一個下界;②函數
的一個下界;②函數![]() 有下界,無上界;
有下界,無上界;
③函數![]() 有上界,無下界;④函數
有上界,無下界;④函數![]() 有界.
有界.
其中所有正確結論的編號為_______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】根據我市房地產數據顯示,今年我市前5個月新建住宅銷售均價逐月上升,為抑制房價過快上漲,政府從6月份開始推出限價房等宏觀調控措施,6月份開始房價得到很好的抑制,房價回落.今年前10個月的房價均價如表:
月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
均價y(萬元/平方米) | 0.83 | 0.95 | 1.00 | 1.05 | 1.17 | 1.15 | 1.10 | 1.06 | 0.98 | 0.94 |
地產數據研究發現,從1月份至5月份的各月均價y(萬元/平方米)與x之間具有正線性相關關系,從6月份至10月份的各月均價y(萬元/平方米)與x之間具有負線性相關關系.
(1)若政府不調控,根據前5個月的數據,求y關于x的回歸直線方程,并預測12月份的房地產均價.(精確到0.01)
(2)政府調控后,從6月份至10月份的數據可得到y與x的回歸直線方程為:![]() .由此預測政府調控后12月份的房地產均價.說明政府調控的必要性.(精確到0.01)
.由此預測政府調控后12月份的房地產均價.說明政府調控的必要性.(精確到0.01)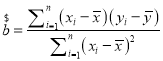 ;
;![]() ;
;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|2x﹣a|+|x﹣a+1|.
(1)當a=4時,求解不等式f(x)≥8;
(2)已知關于x的不等式f(x)![]() 在R上恒成立,求參數a的取值范圍.
在R上恒成立,求參數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為 (
(![]() 為參數),以坐標原點為極點,
為參數),以坐標原點為極點,![]() 軸正半軸為極軸建立極坐標系.曲線
軸正半軸為極軸建立極坐標系.曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的普通方程,曲線
的普通方程,曲線![]() 的參數方程;
的參數方程;
(2)若![]() 分別為曲線
分別為曲線![]() ,
,![]() 上的動點,求
上的動點,求![]() 的最小值,并求
的最小值,并求![]() 取得最小值時,
取得最小值時,![]() 點的直角坐標.
點的直角坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com