
【題目】某品牌汽車4S店對最近100位采用分期付款的購車者進(jìn)行統(tǒng)計,統(tǒng)計結(jié)果如下表所示:
付款方式 | 分1期 | 分2期 | 分3期 | 分4期 | 分5期 |
頻數(shù) | 40 | 20 |
| 10 |
|
已知分3期付款的頻率為0.2,4s店經(jīng)銷一輛該品牌的汽車,顧客分1期付款,其利潤為1萬元,分2期或3期付款其利潤為1.5萬元,分4期或5期付款,其利潤為2萬元,用Y表示經(jīng)銷一輛汽車的利潤.
(Ⅰ)求上表中![]() 的值;
的值;
(Ⅱ)若以頻率作為概率,求事件![]() :“購買該品牌汽車的3位顧客中,至多有一位采用3期付款”的概率
:“購買該品牌汽車的3位顧客中,至多有一位采用3期付款”的概率![]() ;
;
(Ⅲ)求Y的分布列及數(shù)學(xué)期望EY.
 學(xué)練快車道快樂假期暑假作業(yè)新疆人民出版社系列答案
學(xué)練快車道快樂假期暑假作業(yè)新疆人民出版社系列答案 浙大優(yōu)學(xué)小學(xué)年級銜接導(dǎo)與練浙江大學(xué)出版社系列答案
浙大優(yōu)學(xué)小學(xué)年級銜接導(dǎo)與練浙江大學(xué)出版社系列答案 小學(xué)暑假作業(yè)東南大學(xué)出版社系列答案
小學(xué)暑假作業(yè)東南大學(xué)出版社系列答案 津橋教育暑假拔高銜接廣東人民出版社系列答案
津橋教育暑假拔高銜接廣東人民出版社系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() .
.
(1)求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)當(dāng)![]() 時,求證:對于
時,求證:對于![]() ,
,![]() 恒成立;
恒成立;
(3)若存在![]() ,使得當(dāng)
,使得當(dāng)![]() 時,恒有
時,恒有![]() 成立,試求
成立,試求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=![]() -ln(x+m).
-ln(x+m).
(1)設(shè)x=0是f(x)的極值點,求m,并討論f(x)的單調(diào)性;
(2)當(dāng)m≤2時,證明f(x)>0.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,AB//CD,且![]() .
.

(1)證明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,求二面角A-PB-C的余弦值.
,求二面角A-PB-C的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,四棱錐P-ABCD中,底面ABCD為矩形,PA⊥平面ABCD,E為PD的中點.
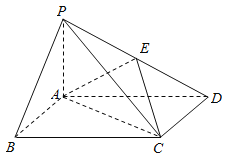
(1) 證明:PB∥平面AEC
(2) 設(shè)二面角D-AE-C為60°,AP=1,AD=![]() ,求三棱錐E-ACD的體積
,求三棱錐E-ACD的體積
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】![]() 是衡量空氣污染程度的一個指標(biāo),為了了解
是衡量空氣污染程度的一個指標(biāo),為了了解![]() 市空氣質(zhì)量情況,從
市空氣質(zhì)量情況,從![]() 年每天的
年每天的![]() 值的數(shù)據(jù)中隨機(jī)抽取
值的數(shù)據(jù)中隨機(jī)抽取![]() 天的數(shù)據(jù),其頻率分布直方圖如圖所示.將
天的數(shù)據(jù),其頻率分布直方圖如圖所示.將![]() 值劃分成區(qū)間
值劃分成區(qū)間![]() 、
、![]() 、
、![]() 、
、![]() ,分別稱為一級、二級、三級和四級,統(tǒng)計時用頻率估計概率 .
,分別稱為一級、二級、三級和四級,統(tǒng)計時用頻率估計概率 .

(1)根據(jù)![]() 年的數(shù)據(jù)估計該市在
年的數(shù)據(jù)估計該市在![]() 年中空氣質(zhì)量為一級的天數(shù);
年中空氣質(zhì)量為一級的天數(shù);
(2)如果![]() 市對環(huán)境進(jìn)行治理,經(jīng)治理后,每天
市對環(huán)境進(jìn)行治理,經(jīng)治理后,每天![]() 值
值![]() 近似滿足正態(tài)分布
近似滿足正態(tài)分布![]() ,求經(jīng)過治理后的
,求經(jīng)過治理后的![]() 值的均值下降率.
值的均值下降率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知點A是雙曲線![]() 的右頂點,若存在過點
的右頂點,若存在過點![]() 的直線與雙曲線的漸近線交于一點M,使得
的直線與雙曲線的漸近線交于一點M,使得![]() 是以點M為直角頂點的直角三角形,則雙曲線的離心率( )
是以點M為直角頂點的直角三角形,則雙曲線的離心率( )
A.存在最大值![]() B.存在最大值
B.存在最大值![]()
C.存在最小值![]() D.存在最小值
D.存在最小值![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】第十三屆全國人民代表大會第二次會議和政協(xié)第十三屆全國委員會第二次會議(簡稱兩會)將分別于![]() 年
年![]() 月
月![]() 日和
日和![]() 月
月![]() 日在北京開幕.全國兩會召開前夕,某網(wǎng)站推出兩會熱點大型調(diào)查,調(diào)查數(shù)據(jù)表明,網(wǎng)約車安全問題是百姓最為關(guān)心的熱點之一,參與調(diào)查者中關(guān)注此問題的約占
日在北京開幕.全國兩會召開前夕,某網(wǎng)站推出兩會熱點大型調(diào)查,調(diào)查數(shù)據(jù)表明,網(wǎng)約車安全問題是百姓最為關(guān)心的熱點之一,參與調(diào)查者中關(guān)注此問題的約占![]() .現(xiàn)從參與者中隨機(jī)選出
.現(xiàn)從參與者中隨機(jī)選出![]() 人,并將這
人,并將這![]() 人按年齡分組:第
人按年齡分組:第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,得到的頻率分布直方圖如圖所示:
,得到的頻率分布直方圖如圖所示:

(1)現(xiàn)在要從年齡較小的第![]() ,
,![]() ,
,![]() 組中用分層抽樣的方法抽取
組中用分層抽樣的方法抽取![]() 人,再從這
人,再從這![]() 人中隨機(jī)抽取
人中隨機(jī)抽取![]() 人贈送禮品,求抽取的
人贈送禮品,求抽取的![]() 人中至少有
人中至少有![]() 人年齡在第
人年齡在第![]() 組的概率;
組的概率;
(2)若從所有參與調(diào)查的人中任意選出![]() 人,記關(guān)注網(wǎng)約車安全問題的人數(shù)為
人,記關(guān)注網(wǎng)約車安全問題的人數(shù)為![]() ,求
,求![]() 的分布列與期望;
的分布列與期望;
(3)把年齡在第![]() ,
,![]() ,
,![]() 組的人稱為青少年組,年齡在第
組的人稱為青少年組,年齡在第![]() ,
,![]() 組的人稱為中老年組,若選出的
組的人稱為中老年組,若選出的![]() 人中不關(guān)注網(wǎng)約車安全問題的人中老年人有
人中不關(guān)注網(wǎng)約車安全問題的人中老年人有![]() 人,問是否有
人,問是否有![]() 的把握認(rèn)為是否關(guān)注網(wǎng)約車安全問題與年齡有關(guān)?附:
的把握認(rèn)為是否關(guān)注網(wǎng)約車安全問題與年齡有關(guān)?附:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
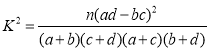 ,
,![]()
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com