
【題目】已知函數(shù)y=x+![]() 有如下性質(zhì):如果常數(shù)t>0,那么該函數(shù)在(0,
有如下性質(zhì):如果常數(shù)t>0,那么該函數(shù)在(0, ![]() ]上是減函數(shù),在[
]上是減函數(shù),在[![]() ,+∞)上是增函數(shù).
,+∞)上是增函數(shù).
(1)已知f(x)=![]() ,x∈[0,1],利用上述性質(zhì),求函數(shù)f(x)的單調(diào)區(qū)間和值域;
,x∈[0,1],利用上述性質(zhì),求函數(shù)f(x)的單調(diào)區(qū)間和值域;
(2)對于(1)中的函數(shù)f(x)和函數(shù)g(x)=-x-2a,若對任意x1∈[0,1],總存在x2∈[0,1],使得g(x2)=f(x1)成立,求實數(shù)a的值.
【答案】(1) [-4,-3] ;(2) a=![]()
【解析】試題分析:(1)f(x)=![]() =
=![]() ,換元后
,換元后![]()
結(jié)合所給性質(zhì)易得所求;(2)對任意x1∈[0,1],總存在x2∈[0,1],使得g(x2)=f(x1)成立等價于f(x)的值域是g(x)的值域的子集.
試題解析:
(1)y=f(x)=![]() =
=![]() ,
,
設(shè)u=2x+1,x∈[0,1],1≤u≤3,
則y=u+![]() -8,u∈[1,3].
-8,u∈[1,3].
由已知性質(zhì)得,當(dāng)1≤u≤2,即0≤x≤![]() 時,f(x)單調(diào)遞減;
時,f(x)單調(diào)遞減;
所以減區(qū)間為[0, ![]() ];
];
當(dāng)2≤u≤3,即![]() ≤x≤1時,f(x)單調(diào)遞增;
≤x≤1時,f(x)單調(diào)遞增;
所以增區(qū)間為[![]() ,1];
,1];
由f(0)=-3,f(![]() )=-4,f(1)=-
)=-4,f(1)=-![]() ,
,
得f(x)的值域為[-4,-3].
(2)g(x)=-x-2a為減函數(shù),
故g(x)∈[-1-2a,-2a],x∈[0,1].
由題意,f(x)的值域是g(x)的值域的子集,
∴![]() ∴a=
∴a=![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為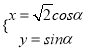 (
(![]() 為參數(shù)),以原點
為參數(shù)),以原點![]() 為極點,
為極點, ![]() 軸正半軸為極軸,建立極坐標(biāo)系,直線
軸正半軸為極軸,建立極坐標(biāo)系,直線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)求曲線![]() 的普通方程與直線
的普通方程與直線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)設(shè)![]() 為曲線
為曲線![]() 上的動點,求點
上的動點,求點![]() 的直線
的直線![]() 的距離的最小值.
的距離的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
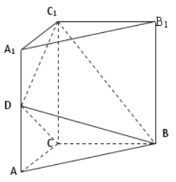
【題目】如圖,三棱柱![]() 的底面是邊長為2的正三角形且側(cè)棱垂直于底面,側(cè)棱長是
的底面是邊長為2的正三角形且側(cè)棱垂直于底面,側(cè)棱長是![]() ,
, ![]() 是
是![]() 的中點.
的中點.

(1)求證: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的大小;
的大小;
(3)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】國際奧委會將于2017年9月15日在秘魯利馬召開130次會議決定2024年第33屆奧運會舉辦地。目前德國漢堡、美國波士頓等申辦城市因市民擔(dān)心賽事費用超支而相繼退出。某機構(gòu)為調(diào)查我國公民對申辦奧運會的態(tài)度,選了某小區(qū)的100位居民調(diào)查結(jié)果統(tǒng)計如下:

(1)根據(jù)已有數(shù)據(jù),把表格數(shù)據(jù)填寫完整;
(2)能否在犯錯誤的概率不超過5%的前提下認為不同年齡與支持申辦奧運無關(guān)?
(3)已知在被調(diào)查的年齡大于50歲的支持者中有5名女性,其中2位是女教師,現(xiàn)從這5名女性中隨機抽取3人,求至多有1位教師的概率.
附:  ,
, ![]() .
.
![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)U=R,集合A={x|x2+3x+2=0},B={x|x2+(m+1)x+m=0},若(![]() A)∩B=,求m的值.
A)∩B=,求m的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() (
(![]() 為常數(shù),
為常數(shù),![]() =2.71828……是自然對數(shù)的底數(shù)),曲線
=2.71828……是自然對數(shù)的底數(shù)),曲線![]() 在點
在點![]() 處的切線與
處的切線與![]() 軸平行.
軸平行.
(1)求![]() 的值;
的值;
(2)求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(3)設(shè)![]() ,其中
,其中![]() 是
是![]() 的導(dǎo)函數(shù).證明:對任意
的導(dǎo)函數(shù).證明:對任意![]() >0,
>0,![]() <
<![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,三棱柱![]() 中,側(cè)棱垂直底面,
中,側(cè)棱垂直底面,![]() ,
,![]() ,
,![]() 是棱
是棱![]() 的中點.
的中點.
(Ⅰ)證明:平面![]() 平面
平面![]() .
.
(Ⅱ)平面![]() 分此棱柱為兩部分,求這兩部分體積比.
分此棱柱為兩部分,求這兩部分體積比.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在多面體ABCDEF中,底面ABCD是梯形,四邊形ADEF是正方形,AB∥DC,AB=AD=1,CD=2,AC=EC=![]() 。
。
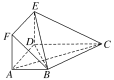
(1)求證:平面EBC⊥平面EBD;
(2)設(shè)M為線段EC上一點,且3EM=EC,試問在線段BC上是否存在一點T,使得MT∥平面BDE,若存在,試指出點T的位置;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() ,函數(shù)
,函數(shù)![]() .
.
(1)當(dāng)![]() 時,解不等式
時,解不等式![]() ;
;
(2)若![]() 在
在![]() 恒成立,求
恒成立,求![]() 的取值范圍;
的取值范圍;
(3)若關(guān)于![]() 的方程
的方程![]() 在區(qū)間
在區(qū)間![]() 內(nèi)的解恰有一個,求
內(nèi)的解恰有一個,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com