
【題目】設![]() ,
, ![]() .
.
(1)若![]() ,求
,求![]() 的單調區間;
的單調區間;
(2)討論![]() 在區間
在區間![]() 上的極值點個數;
上的極值點個數;
(3)是否存在![]() ,使得
,使得![]() 在區間
在區間![]() 上與
上與![]() 軸相切?若存在,求出所有
軸相切?若存在,求出所有![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
【答案】(1)減區間為![]() ,增區間為
,增區間為![]() (2)見解析(3)
(2)見解析(3)![]()
【解析】試題分析:(1)先求函數![]() 導數,再求導函數零點,列表分析導函數符號變化規律,確定單調區間(2)先求函數
導數,再求導函數零點,列表分析導函數符號變化規律,確定單調區間(2)先求函數![]() 導數,轉化為研究
導數,轉化為研究![]() 零點個數,利用二次求導易得
零點個數,利用二次求導易得![]() 在區間
在區間![]() 上單調遞增,其零點個數決定于最小值的大小,討論其最小值與零的大小得到極值點個數, (3)由題意得
上單調遞增,其零點個數決定于最小值的大小,討論其最小值與零的大小得到極值點個數, (3)由題意得![]() 在區間
在區間![]() 上與
上與![]() 軸相切切點為極值點
軸相切切點為極值點![]() ,由(2)得
,由(2)得![]() ,再根據極值點定義可得方程組
,再根據極值點定義可得方程組![]() ,解得
,解得![]()
試題解析:解:(1)當![]() 時:
時:![]() ,(
,(![]() )
)
故![]()
![]()
當![]() 時:
時:![]() ,當
,當![]() 時:
時:![]() ,當
,當![]() 時:
時:![]() .
.
故![]() 的減區間為:
的減區間為:![]() ,增區間為
,增區間為![]()
(2)![]()
令![]()
![]() ,故
,故![]() ,
,![]() ,
,
顯然![]() ,又當
,又當![]() 時:
時:![]() .當
.當![]() 時:
時:![]() .
.
故![]()
![]() ,
,![]()
![]() ,
,![]() .
.
故![]() 在區間
在區間![]() 上單調遞增,
上單調遞增,
注意到:當![]() 時,
時,![]()
![]() ,故
,故![]() 在
在![]() 上的零點個數由
上的零點個數由![]() 的符號決定.
的符號決定.
①當![]() ,即:
,即:![]() 或
或![]() 時:
時:![]() 在區間
在區間![]() 上無零點,即
上無零點,即![]() 無極值點.
無極值點.
②當![]() ,即:
,即:![]() 時:
時:![]() 在區間
在區間![]() 上有唯一零點,即
上有唯一零點,即![]() 有唯一極值點.
有唯一極值點.
綜上:當![]() 或
或![]() 時:
時:![]() 在
在![]() 上無極值點.
上無極值點.
當![]() 時:
時:![]() 在
在![]() 上有唯一極值點.
上有唯一極值點.
(3)假設存在![]() ,使得
,使得![]() 在區間
在區間![]() 上與
上與![]() 軸相切,則
軸相切,則![]() 必與
必與![]() 軸相切于極值點處,
軸相切于極值點處,
由(2)可知:![]() .不妨設極值點為
.不妨設極值點為![]() ,則有:
,則有:
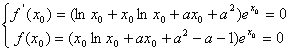 …(*)同時成立.
…(*)同時成立.
聯立得:![]() ,即
,即![]() 代入(*)可得
代入(*)可得![]() .
.
令![]() ,
,![]() .
.
則![]() ,
,![]() ,當
,當 ![]() 時
時![]() (
(![]()
![]()
![]() 2).
2).
故![]() 在
在![]() 上單調遞減.又
上單調遞減.又![]() ,
, ![]() .
.
故![]() 在
在![]() 上存在唯一零點
上存在唯一零點![]() .
.
即當![]() 時
時![]() ,
,![]() 單調遞增.當
單調遞增.當![]() 時
時![]() ,
,![]() 單調遞減.
單調遞減.
因為![]() ,
,![]() .
.
故![]() 在
在![]() 上無零點,在
上無零點,在![]() 上有唯一零點.
上有唯一零點.
由觀察易得![]() ,故
,故![]() ,即:
,即:![]() .
.
綜上可得:存在唯一的![]() 使得
使得![]() 在區間
在區間![]() 上與
上與![]() 軸相切.
軸相切.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x|(x﹣a),a為實數.
(1)若函數f(x)為奇函數,求實數a的值;
(2)若函數f(x)在[0,2]為增函數,求實數a的取值范圍;
(3)是否存在實數a(a<0),使得f(x)在閉區間 ![]() 上的最大值為2,若存在,求出a的值;若不存在,請說明理由.
上的最大值為2,若存在,求出a的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合A={x||x﹣a|≤3,x∈R},B={x|x2﹣3x﹣4>0,x∈R}.
(1)若a=1,求A∩B;
(2)若A∪B=R,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=log3x.
(1)求f(45)﹣f(5)的值;
(2)若函數y=g(x)(x∈R)是奇函數,當x>0時,g(x)=f(x),求函數 y=g(x)的表達式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知各項均為整數的數列{an}滿足an2≤1,1≤a12+a22+…+an2≤m,m,n∈N* .
(1)若m=1,n=2,寫出所有滿足條件的數列{an};
(2)設滿足條件的{an}的個數為f(n,m).
①求f(2,2)和f(2016,2016);
②若f(m+1,m)>2016,試求m的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某影院為了宣傳影片《戰狼Ⅱ》,準備采用以下幾種方式來擴大影響,吸引市民到影院觀看影片,根據以往經驗,預測:
①分發宣傳單需要費用1.5萬元,可吸引30%的市民,增加收入4萬元;
②網絡上宣傳,需要費用8千元,可吸引20%的市民,增加收入3萬元;
③制作小視頻上傳微信群,需要費用2.5萬元,可吸引35%的市民,增加收入5.5萬元;
④與商場合作需要費用1萬元,購物滿800元者可免費觀看影片(商場購票),可吸收15%的市民,增加收入2.5萬元,
問: (1)在三個觀看影片的市民中,至少有一個是通過微信群宣傳方式吸引來的概率是多少?
(2)影院預計可增加盈利是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某倉庫為了保持庫內的濕度和溫度,四周墻上均裝有如圖所示的自動通風設施.該設施的下部ABCD是矩形,其中AB=2米,BC=1米;上部CDG是等邊三角形,固定點E為AB的中點.△EMN是由電腦控制其形狀變化的三角通風窗(陰影部分均不通風),MN是可以沿設施邊框上下滑動且始終保持和AB平行的伸縮橫桿. 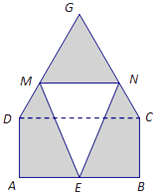
(1)設MN與AB之間的距離為x米,試將△EMN的面積S(平方米)表示成關于x的函數;
(2)求△EMN的面積S(平方米)的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“累積凈化量![]() ”是空氣凈化器質量的一個重要衡量指標,它是指空氣凈化從開始使用到凈化效率為50%時對顆粒物的累積凈化量,以克表示,根據
”是空氣凈化器質量的一個重要衡量指標,它是指空氣凈化從開始使用到凈化效率為50%時對顆粒物的累積凈化量,以克表示,根據![]() 《空氣凈化器》國家標準,對空氣凈化器的累計凈化量
《空氣凈化器》國家標準,對空氣凈化器的累計凈化量![]() 有如下等級劃分:
有如下等級劃分:
累積凈化量(克) |
|
|
| 12以上 |
等級 |
|
|
|
|
為了了解一批空氣凈化器(共5000臺)的質量,隨機抽取![]() 臺機器作為樣本進行估計,已知這
臺機器作為樣本進行估計,已知這![]() 臺機器的累積凈化量都分布在區間
臺機器的累積凈化量都分布在區間![]() 中,按照
中,按照![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 均勻分組,其中累積凈化量在
均勻分組,其中累積凈化量在![]() 的所有數據有:4.5,4.6,5.2,5.3,5.7和5.9,并繪制了頻率分布直方圖,如圖所示:
的所有數據有:4.5,4.6,5.2,5.3,5.7和5.9,并繪制了頻率分布直方圖,如圖所示:
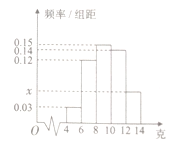
(1)求![]() 的值及頻率分布直方圖中
的值及頻率分布直方圖中![]() 的值;
的值;
(2)以樣本估計總體,試估計這批空氣凈化器(共5000臺)中等級為![]() 的空氣凈化器有多少臺?
的空氣凈化器有多少臺?
(3)從累積凈化量在![]() 的樣本中隨機抽取2臺,求恰好有1臺等級為
的樣本中隨機抽取2臺,求恰好有1臺等級為![]() 的概率.
的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com