
【題目】如圖,C、D是離心率為![]() 的橢圓的左、右頂點,
的橢圓的左、右頂點,![]() 、
、![]() 是該橢圓的左、右焦點, A、B是直線
是該橢圓的左、右焦點, A、B是直線![]() 4上兩個動點,連接AD和BD,它們分別與橢圓交于點E、F兩點,且線段EF恰好過橢圓的左焦點
4上兩個動點,連接AD和BD,它們分別與橢圓交于點E、F兩點,且線段EF恰好過橢圓的左焦點![]() . 當(dāng)
. 當(dāng)![]() 時,點E恰為線段AD的中點.
時,點E恰為線段AD的中點.
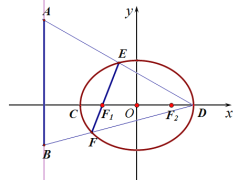
(Ⅰ)求橢圓的方程;
(Ⅱ)求證:以AB為直徑的圓始終與直線EF相切.
【答案】(Ⅰ)![]() (Ⅱ)見證明
(Ⅱ)見證明
【解析】
(Ⅰ)由題意可得![]() ,結(jié)合
,結(jié)合![]() 可求出
可求出![]() ,進(jìn)而可求得橢圓的方程;(Ⅱ)設(shè)EF的方程為:
,進(jìn)而可求得橢圓的方程;(Ⅱ)設(shè)EF的方程為:![]() ,E(
,E(![]() )、F(
)、F(![]() ),與橢圓聯(lián)立,運用韋達(dá)定理得
),與橢圓聯(lián)立,運用韋達(dá)定理得![]() ,
,![]() ,又設(shè)
,又設(shè)![]() ,由三點共線得
,由三點共線得![]() ,
,![]() ,求出
,求出![]() 中點
中點![]() 坐標(biāo)
坐標(biāo)![]() ,求出點M到直線EF的距離
,求出點M到直線EF的距離![]() ,進(jìn)而證得結(jié)果.
,進(jìn)而證得結(jié)果.
(Ⅰ)∵當(dāng)![]() 時,點E恰為線段AD的中點,
時,點E恰為線段AD的中點,
∴![]() ,又
,又![]() ,聯(lián)立解得:
,聯(lián)立解得:![]() ,
,![]() ,
,![]() ,
,
∴橢圓的方程為![]() .
.
(Ⅱ)設(shè)EF的方程為:![]() ,E(
,E(![]() )、F(
)、F(![]() ),
),
 聯(lián)立得:
聯(lián)立得:![]()
∴![]() ,
,
∴ ……(*)
……(*)
又設(shè)![]() ,由A、E、D三點共線得
,由A、E、D三點共線得![]() ,同理可得
,同理可得![]() .
.
 ,
,
∴ .
.
設(shè)AB中點為M,則M坐標(biāo)為(![]() )即(
)即(![]()
![]() ),
),
∴點M到直線EF的距離![]() .
.
故以AB為直徑的圓始終與直線EF相切.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】(本小題滿分14分)如圖,四棱錐![]() 的底面ABCD 是平行四邊形,平面PBD⊥平面 ABCD, PB=PD,
的底面ABCD 是平行四邊形,平面PBD⊥平面 ABCD, PB=PD,![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() ,
,![]() ,
,![]() 分別是
分別是![]() ,
,![]() 的中點,連結(jié)
的中點,連結(jié)![]() .求證:
.求證:
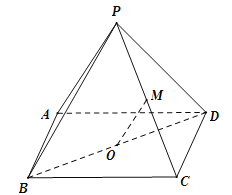
(1)![]() ∥平面
∥平面![]() ;
;
(2)![]() ⊥平面
⊥平面![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若曲線![]() 在點
在點![]() 處的切線方程是
處的切線方程是![]() ,求函數(shù)
,求函數(shù)![]() 在
在![]() 上的值域;
上的值域;
(2)當(dāng)![]() 時,記函數(shù)
時,記函數(shù)![]() ,若函數(shù)
,若函數(shù)![]() 有三個零點,求實數(shù)
有三個零點,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】對于定義在![]() 上的函數(shù)
上的函數(shù)![]() ,若函數(shù)
,若函數(shù)![]() 滿足:①在區(qū)間
滿足:①在區(qū)間![]() 上單調(diào)遞減;②存在常數(shù)
上單調(diào)遞減;②存在常數(shù)![]() ,使其值域為
,使其值域為![]() ,則稱函數(shù)
,則稱函數(shù)![]() 是函數(shù)
是函數(shù)![]() 的“漸近函數(shù)”.
的“漸近函數(shù)”.
(1)求證:函數(shù)![]() 不是函數(shù)
不是函數(shù)![]() 的“漸近函數(shù)”;
的“漸近函數(shù)”;
(2)判斷函數(shù)![]() 是不是函數(shù)
是不是函數(shù)![]() ,
,![]() 的“漸近函數(shù)”,并說明理由;
的“漸近函數(shù)”,并說明理由;
(3)若函數(shù)![]() ,
,![]() ,
,![]() ,求證:
,求證:![]() 是函數(shù)
是函數(shù)![]() 的“漸近函數(shù)”充要條件是
的“漸近函數(shù)”充要條件是![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在第十五次全國國民閱讀調(diào)查中,某地區(qū)調(diào)查組獲得一個容量為![]() 的樣本,其中城鎮(zhèn)居民
的樣本,其中城鎮(zhèn)居民![]() 人,農(nóng)村居民
人,農(nóng)村居民![]() 人.在這些居民中,經(jīng)常閱讀的城鎮(zhèn)居民
人.在這些居民中,經(jīng)常閱讀的城鎮(zhèn)居民![]() 人,農(nóng)村居民
人,農(nóng)村居民![]() 人.
人.
(Ⅰ)填寫下面列聯(lián)表,并判斷是否有![]() 的把握認(rèn)為,經(jīng)常閱讀與居民居住地有關(guān)?
的把握認(rèn)為,經(jīng)常閱讀與居民居住地有關(guān)?
城鎮(zhèn)居民 | 農(nóng)村居民 | 合計 | |
經(jīng)常閱讀 |
|
| |
不經(jīng)常閱讀 | |||
合計 |
|
(Ⅱ)從該地區(qū)居民城鎮(zhèn)的居民中,隨機(jī)抽取![]() 位居民參加一次閱讀交流活動,記這
位居民參加一次閱讀交流活動,記這![]() 位居民中經(jīng)常閱讀的人數(shù)為
位居民中經(jīng)常閱讀的人數(shù)為![]() ,若用樣本的頻率作為概率,求隨機(jī)變量
,若用樣本的頻率作為概率,求隨機(jī)變量![]() 的分布列和期望.
的分布列和期望.
附: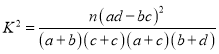 ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】地球海洋面積遠(yuǎn)遠(yuǎn)大于陸地面積,隨著社會的發(fā)展,科技的進(jìn)步,人類發(fā)現(xiàn)海洋不僅擁有巨大的經(jīng)濟(jì)利益,還擁有著深遠(yuǎn)的政治利益.聯(lián)合國于第63屆聯(lián)合國大會上將每年的6月8日確定為“世界海洋日”.2019年6月8日,某大學(xué)的行政主管部門從該大學(xué)隨機(jī)抽取100名大學(xué)生進(jìn)行一次海洋知識測試,并按測試成績(單位:分)分組如下:第一組[65,70),第二組[70,75),第二組[75,80),第四組[80,85),第五組[85,90],得到頻率分布直方圖如下圖:
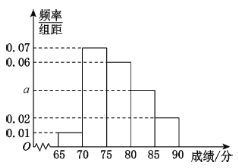
(1)求實數(shù)![]() 的值;
的值;
(2)若從第四組、第五組的學(xué)生中按組用分層抽樣的方法抽取6名學(xué)生組成中國海洋實地考察小隊,出發(fā)前,用簡單隨機(jī)抽樣方法從6人中抽取2人作為正、副隊長,列舉出所有的基本事件并求“抽取的2人為不同組”的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面上給定相異兩點A,B,設(shè)P點在同一平面上且滿足![]() ,當(dāng)
,當(dāng)![]() 且
且![]() 時,P點的軌跡是一個圓,這個軌跡最先由古希臘數(shù)學(xué)家阿波羅尼斯發(fā)現(xiàn),故我們稱這個圓為阿波羅尼斯圓,現(xiàn)有雙曲線
時,P點的軌跡是一個圓,這個軌跡最先由古希臘數(shù)學(xué)家阿波羅尼斯發(fā)現(xiàn),故我們稱這個圓為阿波羅尼斯圓,現(xiàn)有雙曲線![]() (
(![]() ,
,![]() ),A,B為雙曲線的左、右頂點,C,D為雙曲線的虛軸端點,動點P滿足
),A,B為雙曲線的左、右頂點,C,D為雙曲線的虛軸端點,動點P滿足 ,
,![]() 面積的最大值為
面積的最大值為![]() ,
,![]() 面積的最小值為4,則雙曲線的離心率為______.
面積的最小值為4,則雙曲線的離心率為______.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,圓
中,圓![]() 的方程為
的方程為![]() ,且圓
,且圓![]() 與
與![]() 軸交于
軸交于![]() 兩點,設(shè)直線
兩點,設(shè)直線![]() 的方程為
的方程為![]() .
.
(1)當(dāng)直線![]() 與圓
與圓![]() 相切時,求直線
相切時,求直線![]() 的方程;
的方程;
(2)已知直線![]() 與圓
與圓![]() 相交于
相交于![]() 兩點.(i)
兩點.(i)![]() ,求直線
,求直線![]() 的方程;(ii)直線
的方程;(ii)直線![]() 與直線
與直線![]() 相交于點
相交于點![]() ,直線
,直線![]() ,直線
,直線![]() ,直線
,直線![]() 的斜率分別為
的斜率分別為![]() ,
,![]() ,
,![]() ,是否存在常數(shù)
,是否存在常數(shù)![]() ,使得
,使得![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() (
(![]() )經(jīng)過點
)經(jīng)過點![]() ,直線
,直線![]() 與拋物線
與拋物線![]() 有兩個不同的交點
有兩個不同的交點![]() 、
、![]() ,直線
,直線![]() 交
交![]() 軸于
軸于![]() ,直線
,直線![]() 交
交![]() 軸于
軸于![]() .
.
(1)若直線![]() 過點
過點![]() ,求直線
,求直線![]() 的斜率的取值范圍;
的斜率的取值范圍;
(2)若直線![]() 過點
過點![]() ,設(shè)
,設(shè)![]() ,
,![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)若直線![]() 過拋物線
過拋物線![]() 的焦點
的焦點![]() ,交
,交![]() 軸于點
軸于點![]() ,
,![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com