【題目】若數列
、
滿足
(
N*)，則稱為數列的“偏差數列”.
（1）若為常數列，且為的“偏差數列”，試判斷是否一定為等差數列，并說明理由；
（2）若無窮數列是各項均為正整數的等比數列，且
，為數列的“偏差數列”，求
的值；
（3）設
，為數列的“偏差數列”，
，
且
，若
對任意
恒成立，求實數M的最小值.
【答案】（1）見解析；（2）
或
；（3）
【解析】
（1）{an}不一定為等差數列，如
；
（2）設數列{an}的公比為q，解方程可得首項和公比，由等比數列的通項公式和求和公式，計算可得所求值；
（3）由累加法可得數列{an}的通項公式，討論n為奇數或偶數，求得極限，由不等式恒成立思想可得M的最小值．
解：(1) 如
，則
為常數列，但
不是等差數列，
(2) 設數列的公比為
，則由題意，
、均為正整數，
因為
，所以
，
解得
或
，
故
或
(
N*)，
①當時，
，
，
，
② 當時，
，
，
綜上，
的值為或；
(3) 由
≤
且≤
得，
=
故有：
，
，
，
累加得：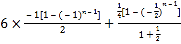
=
=
，
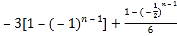
又
，所以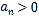
當n為奇數時，單調遞增，
，
，
當n為偶數時，單調遞減，
，
，
從而
≤，所以M≥，即M的最小值為．
科目：高中數學 來源： 題型：
【題目】
在直角坐標系
中，點P到兩點
，
的距離之和等于4，設點P的軌跡為
，直線
與C交于A，B兩點．
（Ⅰ）寫出C的方程；
（Ⅱ）若
，求k的值；
（Ⅲ）若點A在第一象限，證明：當k>0時，恒有||>||．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】用長為18 cm的鋼條圍成一個長方體形狀的框架，要求長方體的長與寬之比為2：1，問該長方體的長、寬、高各為多少時，其體積最大？最大體積是多少？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（本題滿分12分）如圖， 
是圓
的直徑，點
是圓
上異于
的點， 
垂直于圓
所在的平面，且
．
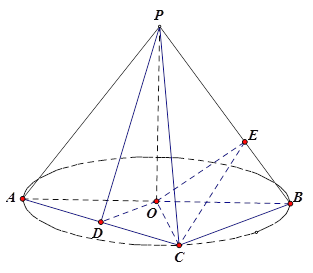
（Ⅰ）若
為線段
的中點，求證
平面
；
（Ⅱ）求三棱錐
體積的最大值；
（Ⅲ）若
，點
在線段
上，求
的最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某賽季甲、乙兩位運動員每場比賽得分的莖葉圖如圖所示.
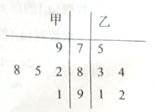
（1）從甲、乙兩人的這5次成績中各隨機抽取一個，求甲的成績比乙的成績高的概率；
（2）試用統計學中的平均數、方差知識對甲、乙兩位運動員的測試成績進行分析.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在直四棱柱ABCD﹣A1B1C1D1中，底面ABCD為菱形，E為DD1中點.
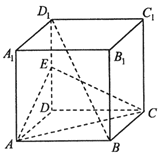
（1）求證：BD1∥平面ACE；
（2）求證：BD1⊥AC.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在平面直角坐標系
中，已知圓
及點
，
．
（1）若直線
平行于
，與圓
相交于
，
兩點，
，求直線
的方程；
（2）在圓
上是否存在點
，使得
？若存在，求點的個數；若不存在，說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在直四棱柱
中，底面
是邊長為2的正方形， 
分別為線段
， 
的中點.
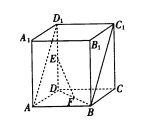
(1)求證： 
||平面
；
(2)四棱柱
的外接球的表面積為
，求異面直線
與
所成的角的大小.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】通過隨機詢問100名性別不同的大學生是否愛好踢毽子，得到如下的列聯表：
隨機變量
經計算，統計量K2的觀測值k0≈4.762，參照附表，得到的正確結論是( )
A. 在犯錯誤的概率不超過5%的前提下，認為“愛好該項運動與性別有關”
B. 在犯錯誤的概率不超過5%的前提下，認為“愛好該項運動與性別無關”
C. 有97.5%以上的把握認為“愛好該項運動與性別有關”
D. 有97.5%以上的把握認為“愛好該項運動與性別無關”
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com