
�O(sh��)ֱ�� �ķ��̞�
�ķ��̞�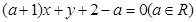 .
.
��1���� �ڃ�����(bi��o)�S�ϵĽؾ���ȣ���
�ڃ�����(bi��o)�S�ϵĽؾ���ȣ��� �ķ��̣�
�ķ��̣�
��2���� ����(j��ng)�^(gu��)�ڶ����ޣ���(sh��)��(sh��)
����(j��ng)�^(gu��)�ڶ����ޣ���(sh��)��(sh��) ��ȡֵ������
��ȡֵ������
��1��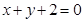 ����2��
����2��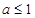 .
.
����ԇ�}��������1����ֱ���Ƿ�(j��ng)�^(gu��)ԭ�c(di��n)�ɷN��rӑՓ���քe��� ��ֵ���Ķ��_��ֱ���ķ��̣�
��ֵ���Ķ��_��ֱ���ķ��̣�
��2����?y��n)�ֱ����б��һ�����ڣ����ԣ���ֱ�����^(gu��)�ڶ����ޣ���ֱ֪����б��ؓ(f��)���� �S�ϵĽؾ����������_����(sh��)��(sh��)��ȡֵ����.
�S�ϵĽؾ����������_����(sh��)��(sh��)��ȡֵ����.
ԇ�}�������⣨1����(d��ng)ֱ���^(gu��)ԭ�c(di��n)�r(sh��)��ԓֱ����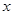 �S��
�S�� �S�ϵĽؾ���㣬��(d��ng)Ȼ��ȣ�
�S�ϵĽؾ���㣬��(d��ng)Ȼ��ȣ�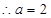 �����̼���
�����̼���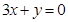 ����
���� ���ɽؾ���ڣ�
���ɽؾ���ڣ�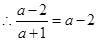 ��
��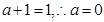 �����̼���
�����̼���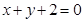 .
.
��2���� �ķ��̻���
�ķ��̻���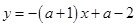 ��
��
���ԣ�Ҫʹ ����(j��ng)�^(gu��)�ڶ����ޣ���(d��ng)�҃H��(d��ng)
����(j��ng)�^(gu��)�ڶ����ޣ���(d��ng)�҃H��(d��ng)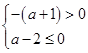 ��
��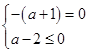
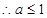
�C�Ͽ�֪ ��ȡֵ������
��ȡֵ������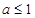 .
.
���c(di��n)��ֱ����һ��ʽ�����c�ؾ�ʽ�Ļ���.


 53�S�Üy(c��)ϵ�д�
53�S�Üy(c��)ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
�o�����タ ��
�� �ǒ��タ
�ǒ��タ �Ľ��c(di��n)���^(gu��)�c(di��n)
�Ľ��c(di��n)���^(gu��)�c(di��n) ��ֱ��
��ֱ�� �c
�c �ཻ��
�ཻ�� ��
�� ���c(di��n)��
���c(di��n)�� ������(bi��o)ԭ�c(di��n).
������(bi��o)ԭ�c(di��n).
��1���O(sh��) ��б�ʞ�1������
��б�ʞ�1������ ��ֱ���ĈA�ķ��̣�
��ֱ���ĈA�ķ��̣�
��2���O(sh��) ����ֱ��
����ֱ�� �ķ���.
�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪�E�A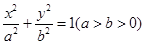 ��һ��(g��)��c(di��n)��B(0��4)���x����
��һ��(g��)��c(di��n)��B(0��4)���x����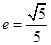 �� ֱ��
�� ֱ��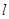 ���E�A��M,N���c(di��n)��
���E�A��M,N���c(di��n)��
��1����ֱ��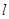 �ķ��̞�y=x-4������MN���L(zh��ng)��
�ķ��̞�y=x-4������MN���L(zh��ng)��
��2�����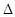 BMN������ǡ�Þ�E�A���ҽ��c(di��n)F����ֱ��
BMN������ǡ�Þ�E�A���ҽ��c(di��n)F����ֱ��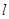 �ķ���.
�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪ ���c(di��n)
���c(di��n) ���ΝM��
���ΝM�� ��
��
(1)���c(di��n) ��܉�E��
��܉�E��
(2)�^(gu��)�c(di��n) ��ֱ��
��ֱ�� ����
���� �齹�c(di��n)�ęE�A��
�齹�c(di��n)�ęE�A�� ���c(di��n)������
���c(di��n)������ �����c(di��n)��
�����c(di��n)�� �S�ľ��x��
�S�ľ��x�� ����ֱ��
����ֱ�� �c�c(di��n)
�c�c(di��n) ��܉�E���У���ԓ�E�A�ķ��̣�
��܉�E���У���ԓ�E�A�ķ��̣�
(3)��(2)�ėl���£��O(sh��)�c(di��n) ������(bi��o)��
������(bi��o)�� ���Ƿ���ڙE�A�ϵ��c(di��n)
���Ƿ���ڙE�A�ϵ��c(di��n) ����
���� ��A�ĵ�һ��(g��)�A��ʹ��ԓ�A�cֱ��
��A�ĵ�һ��(g��)�A��ʹ��ԓ�A�cֱ�� �����У�����ڣ����
�����У�����ڣ���� �c(di��n)����(bi��o)���A�ķ��̣��粻���ڣ�Ո(q��ng)�f(shu��)������.
�c(di��n)����(bi��o)���A�ķ��̣��粻���ڣ�Ո(q��ng)�f(shu��)������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��ֱ֪��l��(j��ng)�^(gu��)ֱ��3x��4y��2��0�cֱ��2x��y��2��0�Ľ��c(di��n)P���Ҵ�ֱ��ֱ��x��2y��1��0 ��
��1����ֱ��l�ķ��̣� ��2����ֱ��l�P(gu��n)��ԭ�c(di��n)O��(du��)�Q��ֱ�����̡�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
ֱ��l1��2x��y��4��0����l1�P(gu��n)��ֱ��l��3x��4y��1��0��(du��)�Q��ֱ��l2�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��ֱ֪��l��(j��ng)�^(gu��)�c(di��n)P(3��1)���ұ���ƽ��ֱ��l1��x��y��1��0��l2��x��y��6��0�صõľ���֮�L(zh��ng)��5����ֱ��l�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪�c(di��n)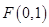 ֱ��
ֱ��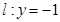 ��
��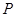 ��ƽ���ϵĄ�(d��ng)�c(di��n)���^(gu��)�c(di��n)
��ƽ���ϵĄ�(d��ng)�c(di��n)���^(gu��)�c(di��n)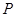 ��ֱ��
��ֱ��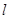 �Ĵ����������
�Ĵ����������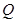 ����
����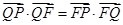 .
.
��1�����(d��ng)�c(di��n)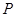 ��܉�E���̣�
��܉�E���̣�
��2��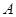 ��
�� ��܉�E
��܉�E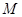 �Ϯ�������(bi��o)ԭ�c(di��n)
�Ϯ�������(bi��o)ԭ�c(di��n) �IJ�ͬ���c(di��n)��܉�E
�IJ�ͬ���c(di��n)��܉�E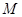 ���c(di��n)
���c(di��n)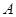 ��
�� ̎���о��քe��
̎���о��քe��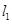 ��
��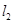 ����
����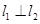 ��
��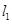 ��
�� �ཻ���c(di��n)
�ཻ���c(di��n) �����c(di��n)
�����c(di��n) �Ŀv����(bi��o).
�Ŀv����(bi��o).
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
б�ʞ� ��ֱ����(j��ng)�^(gu��)�c(di��n)
��ֱ����(j��ng)�^(gu��)�c(di��n) ��ֱ����һ��ʽ������ ��
��ֱ����һ��ʽ������ ��
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com