Question

【題目】已知，，其中，，且函數(shù)在處取得最大值.

（1）求的最小值，并求出此時(shí)函數(shù)的解析式和最小正周期；

（2）在(1)的條件下，先將的圖像上的所有點(diǎn)向右平移個(gè)單位，再把所得圖像上所有點(diǎn)的橫坐標(biāo)伸長(zhǎng)為原來(lái)的2倍(縱坐標(biāo)不變)，然后將所得圖像上所有的點(diǎn)向下平移個(gè)單位，得到函數(shù)的圖像.若在區(qū)間上，方程有兩個(gè)不相等的實(shí)數(shù)根，求實(shí)數(shù)a的取值范圍；

（3）在(1)的條件下，已知點(diǎn)P是函數(shù)圖像上的任意一點(diǎn)，點(diǎn)Q為函數(shù)圖像上的一點(diǎn)，點(diǎn)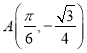，且滿足，求的解集.

Answer 1

【答案】（1）的最小值為1，，，（2）（3）原不等式的解集為

【解析】

（1）先將化成正弦型，然后利用在處取得最大值求出，然后即可得到的解析式和周期

（2）先根據(jù)圖象的變換得到，然后畫出在區(qū)間上的圖象，條件轉(zhuǎn)化為的圖象與直線有兩個(gè)交點(diǎn)即可

（3）利用坐標(biāo)的對(duì)應(yīng)關(guān)系式，求出的函數(shù)的關(guān)系式，進(jìn)一步利用三角不等式的應(yīng)用求出結(jié)果．

（1）因?yàn)?/span>，

所以

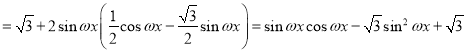
因?yàn)?/span>在處取得最大值.

所以，即

當(dāng)時(shí)的最小值為1

此時(shí)，

（2）將的圖像上的所有的點(diǎn)向右平移個(gè)單位得到的函數(shù)為，再把所得圖像上所有的點(diǎn)的橫坐標(biāo)伸長(zhǎng)為原來(lái)的2倍(縱坐標(biāo)不變)得到的函數(shù)為，然后將所得圖像上所有的點(diǎn)向下平移個(gè)單位，得到函數(shù)

在區(qū)間上的圖象為：

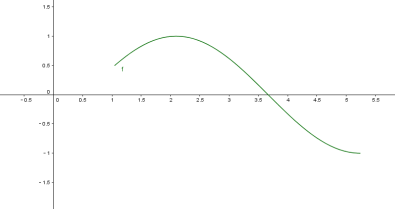
方程有兩個(gè)不相等的實(shí)數(shù)根等價(jià)于的圖象

與直線有兩個(gè)交點(diǎn)

所以，解得

（3）設(shè)，

因?yàn)辄c(diǎn)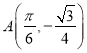，且滿足

所以，所以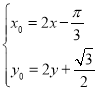

因?yàn)辄c(diǎn)為函數(shù)圖像上的一點(diǎn)

所以

即

因?yàn)?/span>，所以

所以

所以

所以原不等式的解集為