
已知函數
 ,f '(x)為f(x)的導函數,若f '(x)是偶函數且f '(1)=0.
,f '(x)為f(x)的導函數,若f '(x)是偶函數且f '(1)=0.
⑴求函數 的解析式;
的解析式;
⑵若對于區間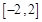 上任意兩個自變量的值
上任意兩個自變量的值 ,都有
,都有 ,求實數
,求實數 的最小值;
的最小值;
⑶若過點
 ,可作曲線
,可作曲線 的三條切線,求實數
的三條切線,求實數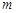 的取值范圍.
的取值范圍.
⑴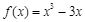 ;⑵
;⑵ 的最小值為
的最小值為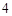 ;⑶
;⑶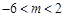 .
.
解析試題分析:⑴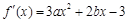 ,由
,由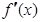 是偶函數得
是偶函數得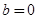 .又
.又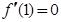 ,所以
,所以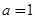 ,由此可得解析式;
,由此可得解析式;
⑵對于區間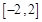 上任意兩個自變量的值
上任意兩個自變量的值 ,都有
,都有 ,則只需
,則只需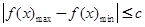 即可.所以接下來就利用導數求
即可.所以接下來就利用導數求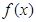 在區間
在區間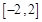 上的最大值與最小值,然后代入
上的最大值與最小值,然后代入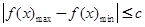 解不等式即可得
解不等式即可得 的最小值.⑶易知點
的最小值.⑶易知點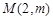
 不在曲線
不在曲線 上.凡是過某點的切線(不是在某點處的切線)的問題,都要設出切點坐標然后列方程組..
上.凡是過某點的切線(不是在某點處的切線)的問題,都要設出切點坐標然后列方程組..
設切點為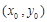 .則
.則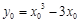 .又
.又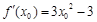 ,∴切線的斜率為
,∴切線的斜率為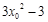 .
.
由此得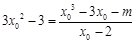 ,即
,即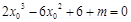 .下面就考查這個方程的解的個數.
.下面就考查這個方程的解的個數.
因為過點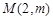
 ,可作曲線
,可作曲線 的三條切線,所以方程
的三條切線,所以方程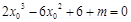 有三個不同的實數解.即函數
有三個不同的實數解.即函數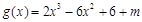 有三個不同的零點.接下來就利用導數結合圖象研究這個函數的零點的個數.
有三個不同的零點.接下來就利用導數結合圖象研究這個函數的零點的個數.
試題解析:⑴∵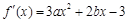 ,1分
,1分
由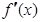 是偶函數得
是偶函數得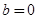 .又
.又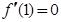 ,所以
,所以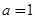 3分
3分
∴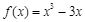 .4分
.4分
⑵令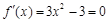 ,即
,即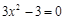 ,解得
,解得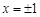 .5分
.5分