
已知函數(shù)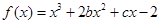 的圖象在與
的圖象在與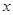 軸交點(diǎn)處的切線方程是
軸交點(diǎn)處的切線方程是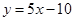 .
.
(I)求函數(shù) 的解析式;
的解析式;
(II)設(shè)函數(shù)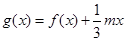 ,若
,若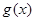 的極值存在,求實(shí)數(shù)
的極值存在,求實(shí)數(shù) 的取值范圍以及函數(shù)
的取值范圍以及函數(shù)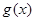 取得極值時(shí)對(duì)應(yīng)的自變量
取得極值時(shí)對(duì)應(yīng)的自變量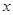 的值.
的值.
(I)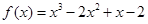 ;(II)
;(II)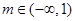 時(shí),函數(shù)
時(shí),函數(shù)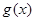 有極值;
有極值;
當(dāng)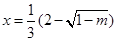 時(shí),
時(shí),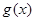 有極大值;當(dāng)
有極大值;當(dāng)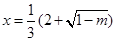 時(shí),
時(shí),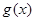 有極小值.
有極小值.
解析試題分析:( I)涉及切線,便要求出切點(diǎn).本題中切點(diǎn)如何求?函數(shù)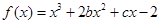 的圖象在與
的圖象在與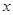 軸交點(diǎn)處的切線方程是
軸交點(diǎn)處的切線方程是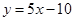 .說明切點(diǎn)就是直線
.說明切點(diǎn)就是直線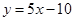 與
與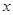 軸交點(diǎn),所以令
軸交點(diǎn),所以令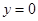 便得切點(diǎn)為(2,0).切點(diǎn)既在切線上又曲線,所以有
便得切點(diǎn)為(2,0).切點(diǎn)既在切線上又曲線,所以有 , 即
, 即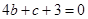 .
.
函數(shù)在切點(diǎn)處的導(dǎo)數(shù)就是切線的斜率,所以由已知有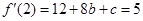 即
即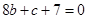 .這樣便得一個(gè)方程組,解這個(gè)方程組求出
.這樣便得一個(gè)方程組,解這個(gè)方程組求出 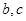 便
便 的解析式.
的解析式.
(II)將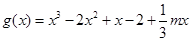 求導(dǎo)得,
求導(dǎo)得,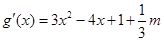 ,
,
令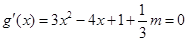 .這是一個(gè)二次方程,要使得函數(shù)有極值,則方程要有兩個(gè)不同的實(shí)數(shù)根,所以
.這是一個(gè)二次方程,要使得函數(shù)有極值,則方程要有兩個(gè)不同的實(shí)數(shù)根,所以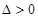 ,由此可得
,由此可得 的范圍.解方程
的范圍.解方程 有便得取得極值時(shí)
有便得取得極值時(shí)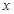 的值.
的值.
試題解析:( I)由已知,切點(diǎn)為(2,0), 故有 , 即
, 即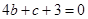
又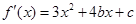 ,由已知
,由已知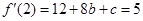 得
得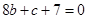
聯(lián)立①②,解得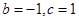 .所以函數(shù)的解析式為
.所以函數(shù)的解析式為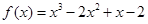
(II)因?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/cc/d/pebuw3.png" style="vertical-align:middle;" />
令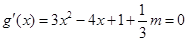
當(dāng)函數(shù)有極值時(shí),則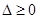 ,方程
,方程 有實(shí)數(shù)解, 由
有實(shí)數(shù)解, 由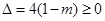 ,得
,得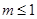 .
.
①當(dāng)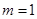 時(shí),
時(shí),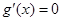 有實(shí)數(shù)
有實(shí)數(shù)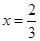 ,在
,在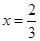 左右兩側(cè)均有
左右兩側(cè)均有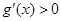 ,故函數(shù)
,故函數(shù)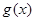 無極值
無極值
②當(dāng)m<1時(shí),g'(x)=0有兩個(gè)實(shí)數(shù)根x1=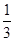 (2
(2 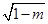 ), x2=
), x2=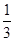 (2+
(2+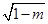 ), g(x),g'(x) 的情況如下表:
), g(x),g'(x) 的情況如下表: