
【題目】將函數(shù) ![]() 的圖象向左平移m(m>0)個單位長度后,所得到的圖象關(guān)于y軸對稱,則m的最小值是( )
的圖象向左平移m(m>0)個單位長度后,所得到的圖象關(guān)于y軸對稱,則m的最小值是( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:y= ![]() cosx+sinx=2(
cosx+sinx=2( ![]() cosx+
cosx+ ![]() sinx)=2sin(x+
sinx)=2sin(x+ ![]() ),
),
∴圖象向左平移m(m>0)個單位長度得到y(tǒng)=2sin[(x+m)+ ![]() ]=2sin(x+m+
]=2sin(x+m+ ![]() ),
),
∵所得的圖象關(guān)于y軸對稱,
∴m+ ![]() =kπ+
=kπ+ ![]() (k∈Z),
(k∈Z),
則m的最小值為 ![]() .
.
故選B
【考點精析】解答此題的關(guān)鍵在于理解兩角和與差的正弦公式的相關(guān)知識,掌握兩角和與差的正弦公式:![]() ,以及對函數(shù)y=Asin(ωx+φ)的圖象變換的理解,了解圖象上所有點向左(右)平移
,以及對函數(shù)y=Asin(ωx+φ)的圖象變換的理解,了解圖象上所有點向左(右)平移![]() 個單位長度,得到函數(shù)
個單位長度,得到函數(shù)![]() 的圖象;再將函數(shù)
的圖象;再將函數(shù)![]() 的圖象上所有點的橫坐標(biāo)伸長(縮短)到原來的
的圖象上所有點的橫坐標(biāo)伸長(縮短)到原來的![]() 倍(縱坐標(biāo)不變),得到函數(shù)
倍(縱坐標(biāo)不變),得到函數(shù)![]() 的圖象;再將函數(shù)
的圖象;再將函數(shù)![]() 的圖象上所有點的縱坐標(biāo)伸長(縮短)到原來的
的圖象上所有點的縱坐標(biāo)伸長(縮短)到原來的![]() 倍(橫坐標(biāo)不變),得到函數(shù)
倍(橫坐標(biāo)不變),得到函數(shù)![]() 的圖象.
的圖象.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在△ABC中,∠C=60°,D是BC上一點,AB=31,BD=20,AD=21. 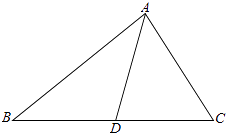
(1)求cos∠B的值;
(2)求sin∠BAC的值和邊BC的長.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,![]() 是東西方向的公路北側(cè)的邊緣線,某公司準(zhǔn)備在
是東西方向的公路北側(cè)的邊緣線,某公司準(zhǔn)備在![]() 上的一點
上的一點![]() 的正北方向的
的正北方向的![]() 處建設(shè)一倉庫,設(shè)
處建設(shè)一倉庫,設(shè)![]() ,并在公路北側(cè)建造邊長為
,并在公路北側(cè)建造邊長為![]() 的正方形無頂中轉(zhuǎn)站
的正方形無頂中轉(zhuǎn)站![]() (其中
(其中![]() 在
在![]() 上),現(xiàn)從倉庫
上),現(xiàn)從倉庫![]() 向
向![]() 和中轉(zhuǎn)站分別修兩條道路
和中轉(zhuǎn)站分別修兩條道路![]() ,已知
,已知![]() ,且
,且![]() .
.

(1)求![]() 關(guān)于
關(guān)于![]() 的函數(shù)解析式,并求出定義域;
的函數(shù)解析式,并求出定義域;
(2)如果中轉(zhuǎn)站四堵圍墻造價為10萬元![]() ,兩條道路造價為30萬元
,兩條道路造價為30萬元![]() ,問:
,問:![]() 取何值時,該公司建設(shè)中轉(zhuǎn)站圍墻和兩條道路總造價
取何值時,該公司建設(shè)中轉(zhuǎn)站圍墻和兩條道路總造價![]() 最低.
最低.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】“紅燈停,綠燈行”,這是我們每個人都應(yīng)該也必須遵守的交通規(guī)則.湊齊一撥人就過馬路﹣﹣不看交通信號燈、隨意穿行交叉路口的“中國式過馬路”不僅不文明而且存在很大的交通安全隱患.一座城市是否存在“中國式過馬路”是衡量這座城市文明程度的重要指標(biāo).某調(diào)查機構(gòu)為了了解路人對“中國式過馬路”的態(tài)度,從馬路旁隨機抽取30名路人進行了問卷調(diào)查,得到了如下列聯(lián)表:
男性 | 女性 | 合計 | |
反感 | 10 | ||
不反感 | 8 | ||
合計 | 30 |
已知在這30人中隨機抽取1人抽到反感“中國式過馬路”的路人的概率是![]() .
.
(1)請將上面的列聯(lián)表補充完整(在答題卷上直接填寫結(jié)果,不需要寫求解過程),并據(jù)此列聯(lián)表數(shù)據(jù)判斷是否有95%的把握認為反感“中國式過馬路”與性別有關(guān)?
(2)若從這30人中的女性路人中隨機抽取2人參加一項活動,記反感“中國式過馬路”的人數(shù)為X,求X的分布列及其數(shù)學(xué)期望.
附:![]() ,其中n=a+b+c+d
,其中n=a+b+c+d
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】對于向量a,b,e及實數(shù)x,y,x1,x2,![]() ,給出下列四個條件:
,給出下列四個條件:
①![]() 且
且![]() ; ②
; ②![]()
③![]() 且
且![]() 唯一; ④
唯一; ④![]()
其中能使a與b共線的是 ( )
A.①②
B.②④
C.①③
D.③④
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]()
(1)若函數(shù)![]() 的圖像在公共點P處有相同的切線,求實數(shù)m的值和P的坐標(biāo);
的圖像在公共點P處有相同的切線,求實數(shù)m的值和P的坐標(biāo);
(2)若函數(shù)![]() 的圖像有兩個不同的交點M、N,求實數(shù)m的取值范圍;
的圖像有兩個不同的交點M、N,求實數(shù)m的取值范圍;
(3)在(2)的條件下,過線段MN的中點作x軸的垂線分別與![]() 的圖像和
的圖像和![]() 的圖象交于S、T點,以S點為切點作
的圖象交于S、T點,以S點為切點作![]() 以T為切點作
以T為切點作![]() 的切線
的切線![]() ,是否存在實數(shù)m,使得
,是否存在實數(shù)m,使得![]() ?如果存在,求出m的值;如果不存在,請說明理由。
?如果存在,求出m的值;如果不存在,請說明理由。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】甲、乙兩校各有3名教師報名支教,期中甲校2男1女,乙校1男2女.
(1)若從甲校和乙校報名的教師中各任選1名,寫出所有可能的結(jié)果,并求選出的2名教師性別相同的概率;
(2)若從報名的6名教師中任選2名,寫出所有可能的結(jié)果,并求選出的2名教師來自同一學(xué)校的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】若定義在R上的函數(shù)![]() 滿足
滿足![]() ,其導(dǎo)函數(shù)
,其導(dǎo)函數(shù)![]() 滿足
滿足![]() ,則下列結(jié)論中一定錯誤的是( )
,則下列結(jié)論中一定錯誤的是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在圓![]() 上任取一點
上任取一點![]() ,過點
,過點![]() 向
向![]() 軸作垂線段
軸作垂線段![]() ,垂足為
,垂足為![]() ,當(dāng)點
,當(dāng)點![]() 在圓上運動時,線段
在圓上運動時,線段![]() 的中點
的中點![]() 的軌跡為
的軌跡為![]() .
.
(1)求曲線![]() 的方程;
的方程;
(2)過點![]() (0,-2)作直線
(0,-2)作直線![]() 與
與![]() 交于
交于![]() 兩點,(O為原點),求三角形
兩點,(O為原點),求三角形![]() 面積的最大值,并求此時的直線
面積的最大值,并求此時的直線![]() 的方程.
的方程.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com