考點:函數恒成立問題
專題:函數的性質及應用
分析:題目給出的函數是分式函數,且分子分母均為二次三項式,對應的函數均開口向上,所以分分子分母對應的方程同解和不同解討論,同解時利用系數相等求a的值,不同解時,若a≠0,則需分子分母對應的方程均無解,a=0時,在定義域內函數值恒大于0.
解答:
解:給出的函數分子分母都是二次三項式,對應的圖象都是開口向上的拋物線,若分子分母對應的方程是同解方程,
則
,解得a=2.
此時函數的值為f(x)=
>0.
若分子分母對應的方程不是同解方程,要保證對于定義域內的任意實數x,函數值均為正,
則需要分子分母的判別式均小于0,
即
| | (a-1)2-4(2-2a)<0 | | a2-4×2×(-2a)<0 |
| |
,
解得-7<a<0.
∴a的范圍是-7<a<0.
當a=0時,函數化為f(x)=
,函數定義域為{x|x≠0},分母恒大于0,分子的判別式小于0,
分子恒大于0,函數值恒正.
綜上,對于定義域內的任意實數x,函數值均為正,則實數a的取值范圍是-7<a≤0或a=2.
故答案為:-7<a≤0或a=2.
點評:本題考查恒成立問題,考查了利用函數值的范圍求解參數的取值范圍,解答此題的關鍵是由函數值恒為正得到分子分母的取值情況,屬中檔題.



 名校課堂系列答案
名校課堂系列答案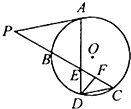 如圖,A是⊙O上的點,PC與⊙O相交于B、C兩點,點D在⊙O上,CD∥AP,AD與BC交于E,F為CE上的點,若∠EDF=∠P,BE=8,EF=4,FC=5,則PB=
如圖,A是⊙O上的點,PC與⊙O相交于B、C兩點,點D在⊙O上,CD∥AP,AD與BC交于E,F為CE上的點,若∠EDF=∠P,BE=8,EF=4,FC=5,則PB=