【題目】已知
，設函數
.
（1）討論
單調性；
（2）若當
時，
，求
的取值范圍.
【答案】（1）見解析；（2）
【解析】
（1）求出函數
的導數，然后根據
的不同取值，進行分類討論函數的單調性；
（2）當
時，
，且
時，
，于是
等價于
，顯然若
，
時，不等式不成立；當若
，構造新函數
，求導，得
，函數
在
單調遞增，所以
，可以證明出當
時，
，當
時，可以通過找到零點，證明出
不恒大于零.
解：（1）
.
當時，
，當
時，
，當
時，
.所以在
單調遞增；在
單調遞減.
當
時，由
得
或
，因為
，所以當或
時，，當
時，.所以在，
單調遞增；在
單調遞減.
（2）當時，，且時，，于是等價于.
若，當時，不成立.
若，設，.
函數在單調遞增，所以.
當時，
，在單調遞增，所以
.
當時，因為
，
，所以存在唯一
，使得當
時，
，在
單調遞減，
，不成立.
綜上，
的取值范圍為
.
科目：高中數學 來源： 題型：
【題目】現代城市大多是棋盤式布局（如北京道路幾乎都是東西和南北走向）.在這樣的城市中，我們說的兩點間的距離往往不是指兩點間的直線距離（位移），而是實際路程（如圖）.在直角坐標平面內，我們定義
，
兩點間的“直角距離”為：
.
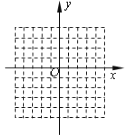
（1）在平面直角坐標系中，寫出所有滿足到原點的“直角距離”為2的“格點”的坐標.（格點指橫、縱坐標均為整數的點）
（2）求到兩定點
、
的“直角距離”和為定值
的動點軌跡方程，并在直角坐標系內作出該動點的軌跡.（在以下三個條件中任選一個做答）
①
，
，
；
②
，
，；
③，，
.
（3）寫出同時滿足以下兩個條件的“格點”的坐標，并說明理由（格點指橫、縱坐標均為整數的點）.
①到
，
兩點“直角距離”相等；
②到
，
兩點“直角距離”和最小.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
是圓
：
上任意一點，
，線段
的垂直平分線與半徑
交于點
，當點在圓上運動時，記點的軌跡為曲線
.
（1）求曲線的方程；
（2）記曲線與
軸交于
兩點，
是直線
上任意一點，直線
，
與曲線的另一個交點分別為
，求證：直線
過定點
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知曲線
的方程為
，集合
，若對于任意的
，都存在
，使得
成立，則稱曲線為
曲線，下列方程所表示的曲線中，是曲線的有______（寫出所有曲線的序號）
①
；②
；③
；④
；⑤
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某小學舉辦“父母養(yǎng)育我，我報父母恩”的活動，對六個年級（一年級到六年級的年級代碼分別為1，2…，6）的學生給父母洗腳的百分比y%進行了調查統(tǒng)計，繪制得到下面的散點圖．
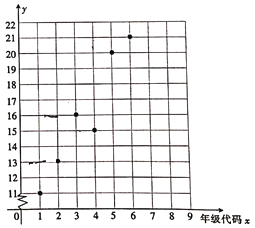
（1）由散點圖看出，可用線性回歸模型擬合y與x的關系，請用相關系數加以說明；
（2）建立y關于x的回歸方程，并據此預計該校學生升入中學的第一年（年級代碼為7）給父母洗腳的百分比．
附注：參考數據：
參考公式：相關系數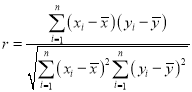
，若r＞0.95，則y與x的線性相關程度相當高，可用線性回歸模型擬合y與x的關系．回歸方程
中斜率與截距的最小二乘估計公式分別為
＝
，
．
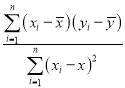查看答案和解析>>
科目：高中數學 來源： 題型：
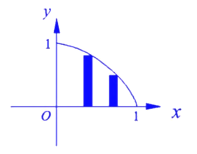
【題目】在平面直角坐標系中，函數
在第一象限內的圖像如圖所示，試做如下操作：把x軸上的區(qū)間
等分成n個小區(qū)間，在每一個小區(qū)間上作一個小矩形，使矩形的右端點落在函數的圖像上.若用
表示第k個矩形的面積，
表示這n個叫矩形的面積總和.
（1）求
的表達式；
（2）利用數學歸納法證明
，并求出的表達式
（3）求
的值，并說明的幾何意義.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
：
，其中
，點
是橢圓的右頂點，射線
：
與橢圓的交點為
.
（1）求點的坐標；
（2）設橢圓的長半軸、短半軸的長分別為
、
，當
的值在區(qū)間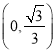
中變化時，求
的取值范圍；
（3）在（2）的條件下，以為焦點，
為頂點且開口方向向左的拋物線過點，求實數
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，對于點
，若函數
滿足：
，都有
，就稱這個函數是點
的“限定函數”．以下函數：①
，②
，③
，④
，其中是原點
的“限定函數”的序號是______．已知點在函數
的圖象上，若函數是點的“限定函數”，則
的取值范圍是______．
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
