
【題目】如圖,正方體![]() 的棱長為
的棱長為![]() ,其中
,其中![]() 為底面
為底面![]() 的中心,
的中心,![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點,平面
的中點,平面![]() 與底面
與底面![]() 交于直線
交于直線![]() .
.
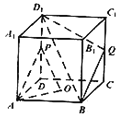
(1)求證:![]() .
.
(2)求點![]() 到平面
到平面![]() 的距離.
的距離.
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某鄉(xiāng)鎮(zhèn)政府為了解決農(nóng)村教師的住房問題,計劃征用一塊土地蓋一幢建筑總面積為10000![]() 公寓樓(每層的建筑面積相同).已知士地的征用費為
公寓樓(每層的建筑面積相同).已知士地的征用費為![]() ,土地的征用面積為第一層的
,土地的征用面積為第一層的![]() 倍,經(jīng)工程技術(shù)人員核算,第一層建筑費用為
倍,經(jīng)工程技術(shù)人員核算,第一層建筑費用為![]() ,以后每增高一層,其建筑費用就增加
,以后每增高一層,其建筑費用就增加![]() ,設(shè)這幢公寓樓高層數(shù)為n,總費用為
,設(shè)這幢公寓樓高層數(shù)為n,總費用為![]() 萬元.(總費用為建筑費用和征地費用之和)
萬元.(總費用為建筑費用和征地費用之和)
(1)若總費用不超過835萬元,求這幢公寓樓最高有多少層數(shù)?
(2)試設(shè)計這幢公寓的樓層數(shù),使總費用最少,并求出最少費用.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() .
.
(1)若![]() 在區(qū)間
在區(qū)間![]() 上不是單調(diào)函數(shù),求實數(shù)
上不是單調(diào)函數(shù),求實數(shù)![]() 的范圍;
的范圍;
(2)若對任意![]() ,都有
,都有![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍;
的取值范圍;
(3)當![]() 時,設(shè)
時,設(shè)![]() ,對任意給定的正實數(shù)
,對任意給定的正實數(shù)![]() ,曲線
,曲線![]() 上是否存在兩點
上是否存在兩點![]() ,
,![]() ,使得
,使得![]() 是以
是以![]() (
(![]() 為坐標原點)為直角頂點的直角三角形,而且此三角形斜邊中點在
為坐標原點)為直角頂點的直角三角形,而且此三角形斜邊中點在![]() 軸上?請說明理由.
軸上?請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標系中,已知直線![]() 的方程為
的方程為![]() ,
,![]() .
.
(1)若直線![]() 在
在![]() 軸、
軸、![]() 軸上的截距之和為-1,求坐標原點
軸上的截距之和為-1,求坐標原點![]() 到直線
到直線![]() 的距離;
的距離;
(2)若直線![]() 與直線
與直線![]() :
:![]() 和
和![]() :
:![]() 分別相交于
分別相交于![]() 、
、![]() 兩點,點
兩點,點![]() 到
到![]() 、
、![]() 兩點的距離相等,求
兩點的距離相等,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某公司為確定下一年度投入某種產(chǎn)品的宣傳費,需了解年宣傳費![]() (單位:千元)對年銷售量
(單位:千元)對年銷售量![]() (單位:
(單位: ![]() )和年利潤
)和年利潤![]() (單位:千元)的影響,對近8年的年宣傳費
(單位:千元)的影響,對近8年的年宣傳費![]() 和年銷售量
和年銷售量![]() 數(shù)據(jù)作了初步處理,得到下面的散點圖及一些統(tǒng)計量的值.
數(shù)據(jù)作了初步處理,得到下面的散點圖及一些統(tǒng)計量的值.

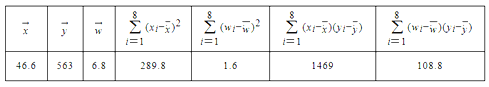
表中![]() ,
,![]() .
.
(1)根據(jù)散點圖判斷, ![]() 與
與![]() 哪一個適宜作為年銷售量
哪一個適宜作為年銷售量![]() 關(guān)于年宣傳費
關(guān)于年宣傳費![]() 的回歸方程類型?(給出判斷即可,不必說明理由)
的回歸方程類型?(給出判斷即可,不必說明理由)
(2)根據(jù)(1)的判斷結(jié)果及表中數(shù)據(jù),建立![]() 關(guān)于
關(guān)于![]() 的回歸方程;
的回歸方程;
(3)已知這種產(chǎn)品的年利潤![]() 與
與![]() 、
、![]() 的關(guān)系為
的關(guān)系為![]() .根據(jù)(2)的結(jié)果要求:年宣傳費
.根據(jù)(2)的結(jié)果要求:年宣傳費![]() 為何值時,年利潤最大?
為何值時,年利潤最大?
附:對于一組數(shù)據(jù)![]() ,
, ![]() ,…,
,…, ![]() 其回歸直線
其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為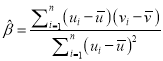 ,
, ![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列命題中是真命題的是![]()
![]()
A. 命題“若![]() ,則
,則![]() ”的否命題是“若
”的否命題是“若![]() ,則
,則![]() ”
”
B. 若![]() 為假命題,則p,q均為假命題
為假命題,則p,q均為假命題
C. 命題p:![]() ,
,![]() ,則
,則![]() :
:![]() ,
,![]()
D. “![]() ”是“函數(shù)
”是“函數(shù)![]() 為偶函數(shù)”的充要條件
為偶函數(shù)”的充要條件
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在Rt△ABC中,AB=BC=4,點E在線段AB上.過點E作EF∥BC交AC于點F,將△AEF沿EF折起到△PEF的位置(點A與P重合),使得∠PEB=60°.

(1)求證:EF⊥PB.
(2)試問:當點E在線段AB上移動時,二面角PFCB的平面角的余弦值是否為定值?若是,求出其定值;若不是,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,ABCD為矩形,點A、E、B、F共面,且![]() 和
和![]() 均為等腰直角三角形,且
均為等腰直角三角形,且![]() 90°.
90°.

(Ⅰ)若平面ABCD![]() 平面AEBF,證明平面BCF
平面AEBF,證明平面BCF![]() 平面ADF;
平面ADF;
(Ⅱ)問在線段EC上是否存在一點G,使得BG∥平面CDF,若存在,求出此時三棱錐G-ABE與三棱錐G-ADF的體積之比.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com