
【題目】某職稱晉級(jí)評(píng)定機(jī)構(gòu)對(duì)參加某次專業(yè)技術(shù)考試的100人的成績(jī)進(jìn)行了統(tǒng)計(jì),繪制了頻率分布直方圖![]() 如圖所示
如圖所示![]() ,規(guī)定80分及以上者晉級(jí)成功,否則晉級(jí)失敗.
,規(guī)定80分及以上者晉級(jí)成功,否則晉級(jí)失敗.
(I) 求圖中a的值;
(II) 根據(jù)已知條件完成下面22列聯(lián)表,并判斷能否有85%的把握認(rèn)為“晉級(jí)成功”與性別有關(guān)?
(III) 將頻率視為概率,從本次考試的所有人員中,隨機(jī)抽取3人進(jìn)行約談,記這3人中晉級(jí)失敗的人數(shù)為X,求X的分布列與數(shù)學(xué)期望E(X).
晉級(jí)成功 | 晉級(jí)失敗 | 合計(jì) | |
男 | 16 | ||
女 | 50 | ||
合計(jì) |

|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() 參考公式:
參考公式:![]() ,其中
,其中![]()
【答案】![]() Ⅰ
Ⅰ![]()
![]() ;
;
![]() Ⅱ
Ⅱ![]() 有超過
有超過![]() 的把握認(rèn)為“晉級(jí)成功”與性別有關(guān);
的把握認(rèn)為“晉級(jí)成功”與性別有關(guān);
![]() Ⅲ
Ⅲ![]() X的分布列為
X的分布列為
X | 0 | 1 | 2 | 3 |
|
|
|
|
|
數(shù)學(xué)期望![]() ,
,
【解析】
(1)根據(jù)頻率和為1,列方程求出a的值;(2)由頻率分布直方圖計(jì)算晉級(jí)成功的頻率,填寫列聯(lián)表,計(jì)算觀測(cè)值![]() ,對(duì)照臨界值得出能有85%的把握認(rèn)為“晉級(jí)成功”與性別有關(guān);(3)用“晉級(jí)失敗”的頻率估計(jì)概率,得
,對(duì)照臨界值得出能有85%的把握認(rèn)為“晉級(jí)成功”與性別有關(guān);(3)用“晉級(jí)失敗”的頻率估計(jì)概率,得![]() ,計(jì)算對(duì)應(yīng)的概率,寫出分布列,計(jì)算數(shù)學(xué)期望值。
,計(jì)算對(duì)應(yīng)的概率,寫出分布列,計(jì)算數(shù)學(xué)期望值。
![]() Ⅰ
Ⅰ![]() 由頻率分布直方圖各小長(zhǎng)方形面積總和為1,
由頻率分布直方圖各小長(zhǎng)方形面積總和為1,
可知![]() ,解得
,解得![]() ;
;
![]() Ⅱ
Ⅱ![]() 由頻率分布直方圖知,晉級(jí)成功的頻率為
由頻率分布直方圖知,晉級(jí)成功的頻率為![]() ,
,
所以晉級(jí)成功的人數(shù)為![]() 人
人![]() ,填表如下:
,填表如下:
晉級(jí)成功 | 晉級(jí)失敗 | 合計(jì) | |
男 | 16 | 34 | 50 |
女 | 9 | 41 | 50 |
合計(jì) | 25 | 75 | 100 |
假設(shè)“晉級(jí)成功”與性別無關(guān),
根據(jù)上表數(shù)據(jù)代入公式可得![]() ,
,
所以有超過![]() 的把握認(rèn)為“晉級(jí)成功”與性別有關(guān);
的把握認(rèn)為“晉級(jí)成功”與性別有關(guān);
![]() Ⅲ
Ⅲ![]() 由頻率分布直方圖知晉級(jí)失敗的頻率為
由頻率分布直方圖知晉級(jí)失敗的頻率為![]() ,
,
將頻率視為概率,則從本次考試的所有人員中,隨機(jī)抽取1人進(jìn)行約談,
這人晉級(jí)失敗的概率為![]() ,所以X可視為服從二項(xiàng)分布,即
,所以X可視為服從二項(xiàng)分布,即![]() ,
,
![]() , 故
, 故![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
所以X的分布列為
X | 0 | 1 | 2 | 3 |
|
|
|
|
|
數(shù)學(xué)期望為![]() , 或
, 或![]()


 新課標(biāo)階梯閱讀訓(xùn)練系列答案
新課標(biāo)階梯閱讀訓(xùn)練系列答案 口算心算速算應(yīng)用題系列答案
口算心算速算應(yīng)用題系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 的導(dǎo)函數(shù)為
的導(dǎo)函數(shù)為![]() ,且
,且![]() ,其中
,其中![]() 為自然對(duì)數(shù)的底數(shù).
為自然對(duì)數(shù)的底數(shù).
(1)求函數(shù)![]() 的最大值;
的最大值;
(2)證明 :![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,平面五邊形ABCDE中,AB∥CE,且AE=2,∠AEC=60°,CD=ED=![]() ,cos∠EDC=
,cos∠EDC=![]() .將△CDE沿CE折起,使點(diǎn)D移動(dòng)到P的位置,且AP=
.將△CDE沿CE折起,使點(diǎn)D移動(dòng)到P的位置,且AP=![]() ,得到四棱錐P-ABCE.
,得到四棱錐P-ABCE.
(1)求證:AP⊥平面ABCE;
(2)記平面PAB與平面PCE相交于直線l,求證:AB∥l.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】蚌埠市某中學(xué)高三年級(jí)從甲(文)、乙(理)兩個(gè)科組各選出![]() 名學(xué)生參加高校自主招生數(shù)學(xué)選拔考試,他們?nèi)〉玫某煽?jī)的莖葉圖如圖所示,其中甲組學(xué)生的平均分是
名學(xué)生參加高校自主招生數(shù)學(xué)選拔考試,他們?nèi)〉玫某煽?jī)的莖葉圖如圖所示,其中甲組學(xué)生的平均分是![]() ,乙組學(xué)生成績(jī)的中位數(shù)是
,乙組學(xué)生成績(jī)的中位數(shù)是![]() .
.
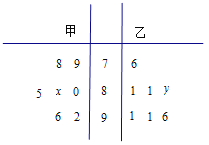
(1)求![]() 和
和![]() 的值;
的值;
(2)計(jì)算甲組![]() 位學(xué)生成績(jī)的方差
位學(xué)生成績(jī)的方差![]() ;
;
(3)從成績(jī)?cè)?/span>![]() 分以上的學(xué)生中隨機(jī)抽取兩名學(xué)生,求甲組至少有一名學(xué)生的概率.
分以上的學(xué)生中隨機(jī)抽取兩名學(xué)生,求甲組至少有一名學(xué)生的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某旅游愛好者計(jì)劃從3個(gè)亞洲國(guó)家A1,A2,A3和3個(gè)歐洲國(guó)家B1,B2,B3中選擇2個(gè)國(guó)家去旅游.
(1)若從這6個(gè)國(guó)家中任選2個(gè),求這2個(gè)國(guó)家都是亞洲國(guó)家的概率;
(2)若從亞洲國(guó)家和歐洲國(guó)家中各選1個(gè),求這兩個(gè)國(guó)家包括A1,但不包括B1的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)系中,以原點(diǎn)為極點(diǎn),x軸的正半軸為極軸建立極坐標(biāo)系,已知曲線C:ρsin2θ=2acos θ(a>0),過點(diǎn)P(-2,-4)的直線l: 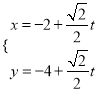 (t為參數(shù))與曲線C相交于M,N兩點(diǎn).
(t為參數(shù))與曲線C相交于M,N兩點(diǎn).
(1)求曲線C的直角坐標(biāo)方程和直線l的普通方程;
(2)若|PM|,|MN|,|PN|成等比數(shù)列,求實(shí)數(shù)a的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知a、b、c為△ABC的三個(gè)內(nèi)角A、B、C的對(duì)邊,向量![]() =(-1,
=(-1,![]() ),
),![]() =(cosA,sinA),若
=(cosA,sinA),若![]() ⊥
⊥![]() ,且acosB+bcosA=csinC,則角B的大小為______.
,且acosB+bcosA=csinC,則角B的大小為______.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]() ,其中
,其中![]() .
.
(1)討論![]() 極值點(diǎn)的個(gè)數(shù);
極值點(diǎn)的個(gè)數(shù);
(2)設(shè)![]() ,函數(shù)
,函數(shù)![]() ,若
,若![]() ,
,![]() (
(![]() )滿足
)滿足![]() 且
且![]() ,證明:
,證明:![]() .
.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com