
【題目】已知![]() .
.
(1)當![]() 為常數(shù),且
為常數(shù),且![]() 在區(qū)間
在區(qū)間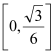 變化時,求
變化時,求![]() 的最小值
的最小值![]() ;
;
(2)證明:對任意的![]() ,總存在
,總存在![]() ,使得
,使得![]() .
.
【答案】(1)![]() ;(2)證明略.
;(2)證明略.
【解析】
試題分析:(1)當![]() 為常數(shù)時,則函數(shù)即為關(guān)于
為常數(shù)時,則函數(shù)即為關(guān)于![]() 的函數(shù),求出此函數(shù)在區(qū)間
的函數(shù),求出此函數(shù)在區(qū)間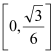 的單調(diào)性,即可求得函數(shù)
的單調(diào)性,即可求得函數(shù)![]() 的最小值
的最小值![]() ;
;
(2)設(shè)![]() ,先求函數(shù)的單調(diào)性,再結(jié)合零點存在性定理,即可證明.
,先求函數(shù)的單調(diào)性,再結(jié)合零點存在性定理,即可證明.
試題解析:(1)當![]() 為常數(shù)時,
為常數(shù)時,
![]() ,
,
![]()
![]() ,
,
當 ,
,![]() 在
在 上遞增,其最小值
上遞增,其最小值![]()
(2)令![]()
![]()
由![]()
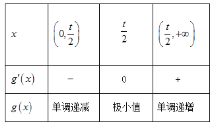
①當![]() ,即
,即![]() 時,
時,![]() 在區(qū)間
在區(qū)間![]() 內(nèi)單調(diào)遞減,
內(nèi)單調(diào)遞減,
![]() ,
,
所以對任意![]() 在區(qū)間
在區(qū)間![]() 內(nèi)均存在零點,即存在
內(nèi)均存在零點,即存在![]() ,使得
,使得![]() .
.
②當![]() ,即
,即![]() 時,
時,![]() 在
在![]() 內(nèi)單調(diào)遞減,在
內(nèi)單調(diào)遞減,在![]() 內(nèi)單調(diào)遞增,
內(nèi)單調(diào)遞增,
所以![]() 時,函數(shù)
時,函數(shù)![]() 取最小值
取最小值![]() ,
,
又![]() ,
,
若![]() ,則
,則![]() ,
,![]() ,
,
所以![]() 在
在![]() 內(nèi)存在零點;
內(nèi)存在零點;
若![]() ,則
,則![]() ,所以
,所以![]() 在
在![]() 內(nèi)存在零點,
內(nèi)存在零點,
所以,對任意![]() 在區(qū)間
在區(qū)間![]() 內(nèi)均存在零點,即存在
內(nèi)均存在零點,即存在![]() ,使得
,使得![]() .
.
結(jié)合①②,對任意的![]() ,總存在
,總存在![]() ,使得
,使得![]() .
.


科目:高中數(shù)學 來源: 題型:
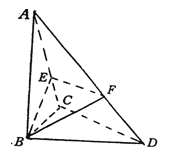
【題目】已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分別是AC、AD上的動點,且![]()
(1)求證:不論![]() 為何值,總有平面BEF⊥平面ABC;
為何值,總有平面BEF⊥平面ABC;
(2)當λ為何值時,平面BEF⊥平面ACD ?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】根據(jù)某電子商務(wù)平臺的調(diào)查統(tǒng)計顯示,參與調(diào)查的1000位上網(wǎng)購物者的年齡情況如圖.
(1)已知![]() 、
、![]() ,
,![]() 三個年齡段的上網(wǎng)購物者人數(shù)成等差數(shù)列,求
三個年齡段的上網(wǎng)購物者人數(shù)成等差數(shù)列,求![]() ,
,![]() 的值;
的值;
(2)該電子商務(wù)平臺將年齡在![]() 之間的人群定義為高消費人群,其他的年齡段定義為潛在消費人群,為了鼓勵潛在消費人群的消費,該平臺決定發(fā)放代金券,高消費人群每人發(fā)放50元的代金券,潛在消費人群每人發(fā)放80元的代金券,已經(jīng)采用分層抽樣的方式從參與調(diào)查的1000位上網(wǎng)購物者中抽取了10人,現(xiàn)在要在這10人中隨機抽取3人進行回訪,求此三人獲得代金券總和
之間的人群定義為高消費人群,其他的年齡段定義為潛在消費人群,為了鼓勵潛在消費人群的消費,該平臺決定發(fā)放代金券,高消費人群每人發(fā)放50元的代金券,潛在消費人群每人發(fā)放80元的代金券,已經(jīng)采用分層抽樣的方式從參與調(diào)查的1000位上網(wǎng)購物者中抽取了10人,現(xiàn)在要在這10人中隨機抽取3人進行回訪,求此三人獲得代金券總和![]() 的分布列與數(shù)學期望.
的分布列與數(shù)學期望.

查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
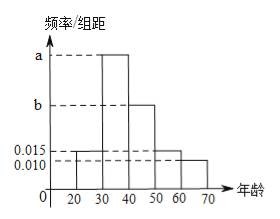
【題目】根據(jù)某電子商務(wù)平臺的調(diào)查統(tǒng)計顯示,參與調(diào)查的![]() 位上網(wǎng)購物者的年齡情況如右圖.
位上網(wǎng)購物者的年齡情況如右圖.
(1)已知![]() 、
、![]() 、
、![]() 三個年齡段的上網(wǎng)購物者人數(shù)成等差數(shù)列,求
三個年齡段的上網(wǎng)購物者人數(shù)成等差數(shù)列,求![]() 的值;
的值;
(2)該電子商務(wù)平臺將年齡在![]() 之間的人群定義為高消費人群,其他的年齡段定義為潛在消費人群,為了鼓勵潛在消費人群的消費,該平臺決定發(fā)放代金券,高消費人群每人發(fā)放
之間的人群定義為高消費人群,其他的年齡段定義為潛在消費人群,為了鼓勵潛在消費人群的消費,該平臺決定發(fā)放代金券,高消費人群每人發(fā)放![]() 元的代金券,潛在消費人群每人發(fā)放
元的代金券,潛在消費人群每人發(fā)放![]() 元的代金券.已經(jīng)采用分層抽樣的方式從參與調(diào)查的
元的代金券.已經(jīng)采用分層抽樣的方式從參與調(diào)查的![]() 位上網(wǎng)購物者中抽取了
位上網(wǎng)購物者中抽取了![]() 人,現(xiàn)在要在這
人,現(xiàn)在要在這![]() 人中隨機抽取
人中隨機抽取![]() 人進行回訪,求此三人獲得代金券總和
人進行回訪,求此三人獲得代金券總和![]() 的分布列與數(shù)學期望.
的分布列與數(shù)學期望.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知等比數(shù)列![]() 滿足
滿足![]() ,數(shù)列
,數(shù)列![]() 滿足
滿足![]() .
.
(1)求數(shù)列![]() ,
, ![]() 的通項公式;
的通項公式;
(2)令![]() ,求數(shù)列
,求數(shù)列![]() 的前
的前![]() 項和
項和![]() ;
;
(3)若![]() ,求對所有的正整數(shù)
,求對所有的正整數(shù)![]() 都有
都有![]() 成立的
成立的![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知向量  ,
, ![]() ,函數(shù)
,函數(shù)![]() 的圖象過點
的圖象過點![]() ,點
,點![]() 與其相鄰的最高點的距離為
與其相鄰的最高點的距離為![]() .
.
(1)求![]() 的單調(diào)遞增區(qū)間;
的單調(diào)遞增區(qū)間;
(2)計算![]() ;
;
(3)設(shè)函數(shù)![]() ,試討論函數(shù)
,試討論函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的零點個數(shù).
上的零點個數(shù).
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設(shè)![]() ,函數(shù)
,函數(shù)![]() ,
,![]() (
(![]() 為自然對數(shù)的底數(shù)),且函數(shù)
為自然對數(shù)的底數(shù)),且函數(shù)![]() 的圖象與函數(shù)
的圖象與函數(shù)![]() 的圖象在
的圖象在![]() 處有公共的切線.
處有公共的切線.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(Ⅲ)證明:當![]() 時,
時,![]() 在區(qū)間
在區(qū)間![]() 內(nèi)恒成立.
內(nèi)恒成立.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,橢圓
,橢圓![]() 和拋物線
和拋物線![]() 交于
交于![]() 兩點,且直線
兩點,且直線![]() 恰好通過橢圓
恰好通過橢圓![]() 的右焦點.
的右焦點.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)經(jīng)過橢圓![]() 右焦點的直線
右焦點的直線![]() 和橢圓
和橢圓![]() 交于
交于![]() 兩點,點
兩點,點![]() 在橢圓上,且
在橢圓上,且![]() ,
,
其中![]() 為坐標原點,求直線
為坐標原點,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com