進(jìn)貨原價(jià)為80元的商品400個，按90元一個售出時，可全部賣出.已知這種商品每個漲價(jià)一元，其銷售數(shù)就減少20個，問售價(jià)應(yīng)為多少時所獲得利潤最大？
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦！ | 初一 | 初一免費(fèi)課程推薦！ |
| 高二 | 高二免費(fèi)課程推薦！ | 初二 | 初二免費(fèi)課程推薦！ |
| 高三 | 高三免費(fèi)課程推薦！ | 初三 | 初三免費(fèi)課程推薦！ |
科目：高中數(shù)學(xué) 來源： 題型：解答題
某投資公司年初用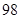
萬元購置了一套生產(chǎn)設(shè)備并即刻生產(chǎn)產(chǎn)品，已知與生產(chǎn)產(chǎn)品相關(guān)的各種配套費(fèi)用第一年需要支出
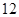萬元，第二年需要支出
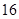萬元，第三年需要支出
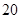萬元，……，每年都比上一年增加支出
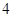萬元，而每年的生產(chǎn)收入都為
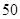萬元．假設(shè)這套生產(chǎn)設(shè)備投入使用
年，
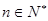，生產(chǎn)成本等于生產(chǎn)設(shè)備購置費(fèi)與這年生產(chǎn)產(chǎn)品相關(guān)的各種配套費(fèi)用的和，生產(chǎn)總利潤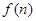
等于這年的生產(chǎn)收入與生產(chǎn)成本的差. 請你根據(jù)這些信息解決下列問題：
（Ⅰ）若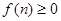
，求的值；
（Ⅱ）若干年后，該投資公司對這套生產(chǎn)設(shè)備有兩個處理方案：
方案一：當(dāng)年平均生產(chǎn)利潤取得最大值時，以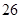
萬元的價(jià)格出售該套設(shè)備；
方案二：當(dāng)生產(chǎn)總利潤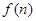取得最大值時，以
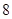萬元的價(jià)格出售該套設(shè)備． 你認(rèn)為哪個方案更合算？請說明理由．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：解答題
“活水圍網(wǎng)”養(yǎng)魚技術(shù)具有養(yǎng)殖密度高、經(jīng)濟(jì)效益好的特點(diǎn)．研究表明：“活水圍網(wǎng)”養(yǎng)魚時，某種魚在一定的條件下，每尾魚的平均生長速度
（單位：千克/年）是養(yǎng)殖密度
（單位：尾/立方米）的函數(shù)．當(dāng)不超過4（尾/立方米）時，的值為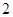
（千克/年）；當(dāng)
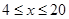時，是的一次函數(shù)；當(dāng)達(dá)到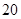
（尾/立方米）時，因缺氧等原因，的值為
（千克/年）．
（1）當(dāng)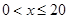
時，求函數(shù)
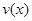的表達(dá)式；
（2）當(dāng)養(yǎng)殖密度為多大時，魚的年生長量（單位：千克/立方米）
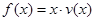可以達(dá)到最大，并求出最大值．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：解答題
某工廠某種產(chǎn)品的年固定成本為250萬元，每生產(chǎn)
千件，需另投入成本為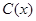
，當(dāng)年產(chǎn)量不足80千件時，
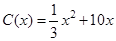（萬元）.當(dāng)年產(chǎn)量不小于80千件時，
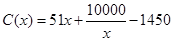（萬元），每件商品售價(jià)為0.05萬元，通過市場分析，該廠生產(chǎn)的商品能全部售完.
（Ⅰ）寫出年利潤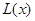
（萬元）關(guān)于年產(chǎn)量（千件）的函數(shù)解析式；
（Ⅱ）年產(chǎn)量為多少千件時，該廠在這一商品的生產(chǎn)中所獲利潤最大？
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：解答題
已知函數(shù)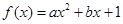
(
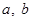為實(shí)數(shù),
,
)，
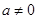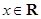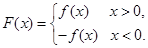
（Ⅰ）若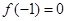
，且函數(shù)
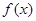的值域?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/ec/24/ec824321244b3975c8c90c0df6fc4502.png" style="vertical-align:middle;" />，求
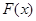的表達(dá)式；
（Ⅱ）在（Ⅰ）的條件下，當(dāng)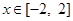
時，
是單調(diào)函數(shù)，求實(shí)數(shù)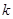
的取值范圍；
（Ⅲ）設(shè)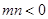
，
，
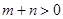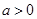，且函數(shù)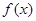為偶函數(shù)，判斷
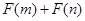是否大于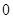
？
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：解答題
已知函數(shù)f(x)＝x2＋2ax＋3，x∈[－4,6]．
(1)當(dāng)a＝－2時，求f(x)的最值；
(2)求實(shí)數(shù)a的取值范圍，使y＝f(x)在區(qū)間[－4,6]上是單調(diào)函數(shù)；
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：解答題
運(yùn)貨卡車以每小時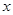
千米的速度勻速行駛130千米
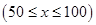（單位：千米/小時）．假設(shè)汽油的價(jià)格是每升2元，而汽車每小時耗油
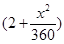升，司機(jī)的工資是每小時14元.
（Ⅰ）求這次行車總費(fèi)用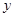
關(guān)于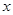的表達(dá)式；
（Ⅱ）當(dāng)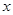為何值時，這次行車的總費(fèi)用最低，并求出最低費(fèi)用的值．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：解答題
某水域一艘裝載濃硫酸的貨船發(fā)生側(cè)翻,導(dǎo)致濃硫酸泄漏,對河水造成了污染.為減
少對環(huán)境的影響，環(huán)保部門迅速反應(yīng),及時向污染河道投入固體堿，個單位的固體堿在水中
逐漸溶化,水中的堿濃度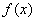
與時間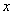
(小時)的關(guān)系可近似地表示為：
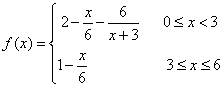,只有當(dāng)污染河道水中堿的濃度不低于
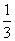時,才能對污
染產(chǎn)生有效的抑制作用.
（1）如果只投放1個單位的固體堿，則能夠維持有效的抑制作用的時間有多長？
（2）第一次投放1單位固體堿后,當(dāng)污染河道水中的堿濃度減少到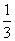時,馬上再投放1個單
位的固體堿,設(shè)第二次投放后水中堿濃度為
,求的函數(shù)式及水中堿濃度的最大值.
（此時水中堿濃度為兩次投放的濃度的累加）
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話：027-86699610 舉報(bào)郵箱：58377363@163.com
時
得
（
，
在
上的單調(diào)；
上的值域是
的值.