
【題目】![]() 是定義在
是定義在![]() 上的奇函數(shù),其圖象如圖所示,令
上的奇函數(shù),其圖象如圖所示,令![]() ,則下列關于函數(shù)
,則下列關于函數(shù)![]() 的敘述正確的是()
的敘述正確的是()

A. 若![]() ,則函數(shù)
,則函數(shù)![]() 的圖象關于原點對稱
的圖象關于原點對稱
B. 若![]() ,則方程
,則方程![]() 有大于2的實根
有大于2的實根
C. 若![]() ,則方程
,則方程![]() 有兩個實根
有兩個實根
D. 若![]() ,則方程
,則方程![]() 有兩個實根
有兩個實根
【答案】B
【解析】
試題奇函數(shù)的圖象關于原點對稱;當a≠0時af(x)與f(x)有相同的奇偶性;f(x)+b的圖象可由f(x)上下平移得到.充分利用以上知識點逐項分析即可解答解:①若a=-1,b=1,則函數(shù)g(x)不是奇函數(shù),其圖象不可能關于原點對稱,所以選項A錯誤;②當a=-1時,-f(x)仍是奇函數(shù),2仍是它的一個零點,但單調性與f(x)相反,若再加b,-2<b<0,則圖象又向下平移-b個單位長度,所以g(x)=-f(x)+b=0有大于2的實根,所以選項B正確;③若a=1,b=2,則g(x)=f(x)+2,其圖象由f(x)的圖象向上平移2個單位長度,那么g(x)只有兩個零點,所以g(x)=0只有兩個實根,所以選項C錯誤;④若a=1,b=-3,則g(x)的圖象由f(x)的圖象向下平移3個單位長度,它只有1個零點,即g(x)=0只有一個實根,所以選項D錯誤.故選B


科目:高中數(shù)學 來源: 題型:
【題目】已知正方形![]() 的對角線
的對角線![]() 與
與![]() 相交于
相交于![]() 點,將
點,將![]() 沿對角線折起,使得平面
沿對角線折起,使得平面![]() 平面
平面![]() (如圖),則下列命題中正確的是( )
(如圖),則下列命題中正確的是( )
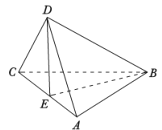
A. 直線![]() 直線
直線![]() ,且直線
,且直線![]() 直線
直線![]()
B. 直線![]() 平面
平面![]() ,且直線
,且直線![]() 平面
平面![]()
C. 平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]()
D. 平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知a>0且a≠1,若函數(shù)f(x)=loga[ax2﹣(2﹣a)x+3]在[ ![]() ,2]上是增函數(shù),則a的取值范圍是 .
,2]上是增函數(shù),則a的取值范圍是 .
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,四棱錐P﹣ABCD中,底面ABCD為菱形,PA⊥平面ABCD,E為PD的中點,F(xiàn)為AC和BD的交點.
(1)證明:PB∥平面AEC;
(2)證明:平面PAC⊥平面PBD.

查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖, ![]() 為坐標原點,雙曲線
為坐標原點,雙曲線![]() 和橢圓
和橢圓![]() 均過點
均過點 ,且以
,且以![]() 的兩個頂點和
的兩個頂點和![]() 的兩個焦點為頂點的四邊形是面積為2的正方形.
的兩個焦點為頂點的四邊形是面積為2的正方形.

(1)求![]() 的方程;
的方程;
(2)是否存在直線![]() ,使得
,使得![]() 與
與![]() 交于
交于![]() 兩點,與
兩點,與![]() 只有一個公共點,且
只有一個公共點,且![]() ?證明你的結論.
?證明你的結論.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知空間中三點A(-2,0,2),B(-1,1,2),C(-3,0,4),設![]() =
=![]() ,
,![]() =
=![]() .
.
(1)求![]() 與
與![]() 的夾角的余弦值; (2)若
的夾角的余弦值; (2)若![]() 與k
與k![]() -2
-2![]() 互相垂直,求實數(shù)k的值.
互相垂直,求實數(shù)k的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】經市場調查,某超市的一種小商品在過去近20天內的日銷售量(件)與價格(元)均為時間t(天)的函數(shù),且日銷售量(件)近似函數(shù)g(t)=80-2t,價格(元)近似滿足函數(shù)關系式為
f(t)=20-![]() |t-10|.
|t-10|.
(1)試寫出該種商品的日銷售額y與時間t(0≤t≤20)的函數(shù)表達式;
(2)求該種商品的日銷售額y的最大值與最小值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com