
【題目】如圖1,在邊長為2的等邊![]() 中,
中,![]() 分別為邊
分別為邊![]() 的中點,將AED沿
的中點,將AED沿![]() 折起,使得
折起,使得![]() ,
, ![]() ,得到如圖2的四棱錐A-BCDE,連結(jié)
,得到如圖2的四棱錐A-BCDE,連結(jié)![]() ,且
,且![]() 與
與![]() 交于點
交于點![]() .
.
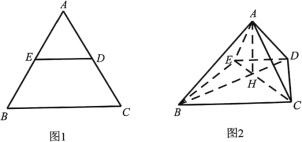
(1)求證:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)詳見解析;(2)![]() .
.
【解析】
(1)由題意可得![]() ,
,![]() ,即可得
,即可得![]() ,
, ![]() ,利用線面垂直的判定即可得證;
,利用線面垂直的判定即可得證;
(2)建立空間直角坐標(biāo)系后,表示出各點坐標(biāo),求出平面![]() 、平面
、平面![]() 的一個法向量為
的一個法向量為![]() 、
、![]() ,利用
,利用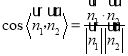 即可得解.
即可得解.
(1)證明:由題意![]() ,
,![]() ,
,
因為![]() 、
、![]() 分別為
分別為![]() 、
、![]() 的中點,
的中點,
所以![]() 且相似比為2,所以
且相似比為2,所以![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
又因為![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,
由![]() 可得
可得![]() 平面
平面![]() ,得證.
,得證.
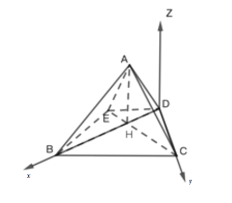
(2)如圖,過D作![]() 平面
平面![]() ,DB為x軸,DC為y軸,Dz為z軸,建立空間直角坐標(biāo)系;
,DB為x軸,DC為y軸,Dz為z軸,建立空間直角坐標(biāo)系;
所以![]() ,
,![]() ,
,![]() ,
,
由(1)知![]() ,則
,則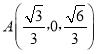 ,
,
由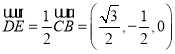 可知
可知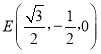 ,
,
所以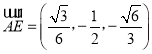 ,
,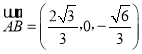 ,
,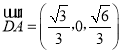 ,
,
設(shè)平面![]() 的一個法向量為
的一個法向量為![]() ,
,
所以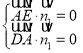 ,即
,即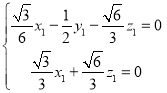 ,取
,取![]() 得
得![]() ,
,
同理可得平面![]() 的一個法向量
的一個法向量![]() ,
,
所以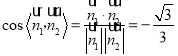 ,
,
由圖可知,所求二面角為鈍角,所以二面角![]() 的余弦值為
的余弦值為![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】對某兩名高三學(xué)生在連續(xù)9次數(shù)學(xué)測試中的成績(單位:分)進(jìn)行統(tǒng)計得到折線圖,下面是關(guān)于這兩位同學(xué)的數(shù)學(xué)成績分析.
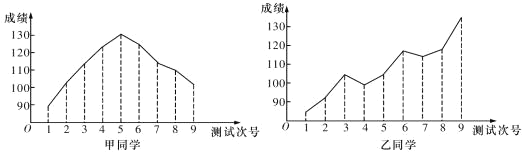
①甲同學(xué)的成績折線圖具有較好的對稱性,故平均成績?yōu)?30分;
②根據(jù)甲同學(xué)成績折線圖提供的數(shù)據(jù)進(jìn)行統(tǒng)計,估計該同學(xué)平均成績在區(qū)間![]() 內(nèi);
內(nèi);
③乙同學(xué)的數(shù)學(xué)成績與測試次號具有比較明顯的線性相關(guān)性,且為正相關(guān);
④乙同學(xué)連續(xù)九次測驗成績每一次均有明顯進(jìn)步.
其中正確的個數(shù)為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為了政府對過熱的房地產(chǎn)市場進(jìn)行調(diào)控決策,統(tǒng)計部門對城市人和農(nóng)村人進(jìn)行了買房的心理預(yù)期調(diào)研,用簡單隨機(jī)抽樣的方法抽取110人進(jìn)行統(tǒng)計,得到如下列聯(lián)表:
買房 | 不買房 | 糾結(jié) | |
城市人 | 5 | 15 | |
農(nóng)村人 | 20 | 10 |
已知樣本中城市人數(shù)與農(nóng)村人數(shù)之比是3:8.
![]() 分別求樣本中城市人中的不買房人數(shù)和農(nóng)村人中的糾結(jié)人數(shù);
分別求樣本中城市人中的不買房人數(shù)和農(nóng)村人中的糾結(jié)人數(shù);
![]() 用獨立性檢驗的思想方法說明在這三種買房的心理預(yù)期中哪一種與城鄉(xiāng)有關(guān)?
用獨立性檢驗的思想方法說明在這三種買房的心理預(yù)期中哪一種與城鄉(xiāng)有關(guān)?
參考公式:![]() .
.
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)系![]() 中,已知點
中,已知點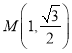 ,
,![]() 的參數(shù)方程為
的參數(shù)方程為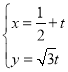 (
(![]() 為參數(shù)),以坐標(biāo)原點
為參數(shù)),以坐標(biāo)原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸,建立極坐標(biāo)系,曲線
軸的正半軸為極軸,建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)設(shè)曲線![]() 與曲線
與曲線![]() 相交于
相交于![]() ,
,![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知點![]() ,
,![]() 分別在
分別在![]() 軸,
軸,![]() 軸上運動,
軸上運動,![]() ,點
,點![]() 在線段
在線段![]() 上,且
上,且![]() .
.
(1)求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)直線![]() 與
與![]() 交于
交于![]() ,
,![]() 兩點,
兩點,![]() ,若直線
,若直線![]() ,
,![]() 的斜率之和為2,直線
的斜率之和為2,直線![]() 是否恒過定點?若是,求出定點的坐標(biāo);若不是,請說明理由.
是否恒過定點?若是,求出定點的坐標(biāo);若不是,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】古希臘數(shù)學(xué)家阿波羅尼奧斯發(fā)現(xiàn):平面上到兩定點![]() ,
,![]() 距離之比為常數(shù)
距離之比為常數(shù)![]() 且
且![]() 的點的軌跡是一個圓心在直線
的點的軌跡是一個圓心在直線![]() 上的圓,該圓簡稱為阿氏圓.根據(jù)以上信息,解決下面的問題:如圖,在長方體
上的圓,該圓簡稱為阿氏圓.根據(jù)以上信息,解決下面的問題:如圖,在長方體![]() 中,
中,![]() ,點
,點![]() 在棱
在棱![]() 上,
上,![]() ,動點
,動點![]() 滿足
滿足![]() .若點
.若點![]() 在平面
在平面![]() 內(nèi)運動,則點
內(nèi)運動,則點![]() 所形成的阿氏圓的半徑為________;若點
所形成的阿氏圓的半徑為________;若點![]() 在長方體
在長方體![]() 內(nèi)部運動,
內(nèi)部運動,![]() 為棱
為棱![]() 的中點,
的中點,![]() 為
為![]() 的中點,則三棱錐
的中點,則三棱錐![]() 的體積的最小值為___________.
的體積的最小值為___________.


查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】甲、乙兩同學(xué)在復(fù)習(xí)數(shù)列時發(fā)現(xiàn)原來曾經(jīng)做過的一道數(shù)列問題因紙張被破壞,導(dǎo)致一個條件看不清,具體如下:等比數(shù)列![]() 的前n項和為
的前n項和為![]() ,已知_____,
,已知_____,
(1)判斷![]() ,
,![]() ,
,![]() 的關(guān)系;
的關(guān)系;
(2)若![]() ,設(shè)
,設(shè)![]() ,記
,記![]() 的前n項和為
的前n項和為![]() ,證明:
,證明:![]() .
.
甲同學(xué)記得缺少的條件是首項a1的值,乙同學(xué)記得缺少的條件是公比q的值,并且他倆都記得第(1)問的答案是![]() ,
,![]() ,
,![]() 成等差數(shù)列.如果甲、乙兩同學(xué)記得的答案是正確的,請你通過推理把條件補(bǔ)充完整并解答此題.
成等差數(shù)列.如果甲、乙兩同學(xué)記得的答案是正確的,請你通過推理把條件補(bǔ)充完整并解答此題.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓C:![]() 1(a
1(a![]() b
b![]() 0)的左、右焦點分別為F1,F2,點P為橢圓C上不與左右頂點重合的動點,設(shè)I,G分別為△PF1F2的內(nèi)心和重心.當(dāng)直線IG的傾斜角不隨著點P的運動而變化時,橢圓C的離心率為_____.
0)的左、右焦點分別為F1,F2,點P為橢圓C上不與左右頂點重合的動點,設(shè)I,G分別為△PF1F2的內(nèi)心和重心.當(dāng)直線IG的傾斜角不隨著點P的運動而變化時,橢圓C的離心率為_____.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com