
【題目】如圖,矩形![]() 所在平面垂直于直角梯形
所在平面垂直于直角梯形![]() 所在平面,
所在平面,![]() ,
,![]() 分別是
分別是![]() 的中點.
的中點.
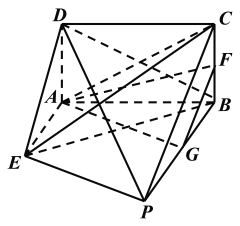
(1)求證:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正切值.
的正切值.
【答案】(1)見解析;(2)![]()
【解析】
(1)由幾何關系可知四邊形![]() 是平行四邊形,則
是平行四邊形,則![]() . 由線面平行的判定定理可得
. 由線面平行的判定定理可得![]() 平面
平面![]() . 由中位線的性質可知
. 由中位線的性質可知![]() ,則
,則![]() 面
面![]() 利用面面平行的判定定理即可證得平面
利用面面平行的判定定理即可證得平面![]() 平面
平面![]() .
.
(2)以![]() 為坐標原點建立空間直角坐標系,計算可得平面
為坐標原點建立空間直角坐標系,計算可得平面![]() 的一個法向量
的一個法向量![]() .而平面
.而平面![]() 的一個法向量為
的一個法向量為![]() .據此可得
.據此可得![]() ,然后結合同角三角函數基本關系求解二面角
,然后結合同角三角函數基本關系求解二面角![]() 的正切值即可.
的正切值即可.
(1)因為![]() 是
是![]() 的中點,
的中點,![]() ,所以
,所以![]() .
.
又因為![]() ,
, ![]() ,所以
,所以![]() ,且
,且![]() ,
,
所以四邊形![]() 是平行四邊形,所以
是平行四邊形,所以![]() .
.
又因為![]() 平面
平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
因為![]() 分別是
分別是![]() 的中點,所以
的中點,所以![]() .
.
又因為![]() 平面
平面![]() 平面
平面![]() ,所以
,所以![]() 面
面![]()
又因為![]() 平面
平面![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
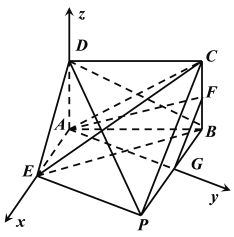
(2)以![]() 為坐標原點建立如圖所示空間直角坐標系,則
為坐標原點建立如圖所示空間直角坐標系,則![]() ,
,
所以![]() .
.
設平面![]() 的一個法向量為
的一個法向量為![]() ,則
,則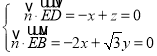 ,令
,令![]() ,得
,得![]() ,
,
所以![]() .
.
易知平面![]() 的一個法向量為
的一個法向量為![]() .
.
所以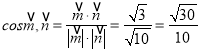 .
.
又因為二面角![]() 的平面角為銳角,所以二面角
的平面角為銳角,所以二面角![]() 的正切值
的正切值![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程是
的參數方程是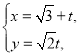 (
(![]() 為參數),曲線
為參數),曲線![]() 的直角坐標方程為
的直角坐標方程為![]() ,將曲線
,將曲線![]() 上的點向下平移1個單位,然后橫坐標伸長為原來的2倍,縱坐標不變,得到曲線
上的點向下平移1個單位,然后橫坐標伸長為原來的2倍,縱坐標不變,得到曲線![]() .
.
(1)求曲線![]() 和曲線
和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若曲線![]() 和曲線
和曲線![]() 相交于
相交于![]() 兩點,求三角形
兩點,求三角形![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學數學老師分別用兩種不同教學方式對入學數學平均分和優秀率都相同的甲、乙兩個高一新班(人數均為![]() 人)進行教學(兩班的學生學習數學勤奮程度和自覺性一致),數學期終考試成績莖葉圖如下:
人)進行教學(兩班的學生學習數學勤奮程度和自覺性一致),數學期終考試成績莖葉圖如下:
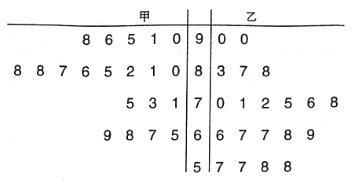
(1)現從乙班數學成績不低于![]() 分的同學中隨機抽取兩名同學,求至少有一名成績為
分的同學中隨機抽取兩名同學,求至少有一名成績為![]() 分的同學被抽中的概率;
分的同學被抽中的概率;
(2)學校規定:成績不低于![]() 分的優秀,請填寫下面的
分的優秀,請填寫下面的![]() 聯表,并判斷有多大把握認為“成績優秀與教學方式有關”.
聯表,并判斷有多大把握認為“成績優秀與教學方式有關”.
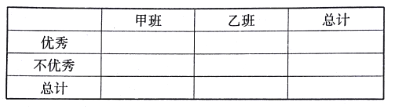
附:參考公式及數據

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某農場計劃設計建造一條2000米長的水渠,其橫斷面如圖所示.其中,底部是半徑為1米的圓弧![]() ,上部是有一定傾角的線段
,上部是有一定傾角的線段![]() 與
與![]() ,渠深
,渠深![]() 為
為![]() 米,且圓弧
米,且圓弧![]() 的圓心為O在
的圓心為O在![]() 上,
上,![]() ,
,![]() ,
,![]() ,
,![]() .據測算,水渠底部曲面每平方米的造價為
.據測算,水渠底部曲面每平方米的造價為![]() 百元,上部矩形壁面每平方米的造價為1百元,其他費用忽略不計.設
百元,上部矩形壁面每平方米的造價為1百元,其他費用忽略不計.設![]() ,
,![]() .
.
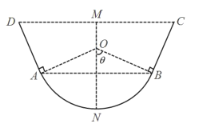
(1)試用![]() 表示水渠建造的總費用
表示水渠建造的總費用![]() (單位:百元);
(單位:百元);
(2)試確定![]() 的值,使得建造總費用最低.
的值,使得建造總費用最低.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地區2020年清明節前后3天每天下雨的概率為60%,通過模擬實驗的方法來計算該地區這3天中恰好有2天下雨的概率:用隨機數![]() (
(![]() ,且
,且![]() )表示是否下雨:當
)表示是否下雨:當![]() 時表示該地區下雨,當
時表示該地區下雨,當![]() 時,表示該地區不下雨,從隨機數表中隨機取得20組數如下
時,表示該地區不下雨,從隨機數表中隨機取得20組數如下
332 714 740 945 593 468 491 272 073 445
992 772 951 431 169 332 435 027 898 719
(1)求出![]() 的值,并根據上述數表求出該地區清明節前后3天中恰好有2天下雨的概率;
的值,并根據上述數表求出該地區清明節前后3天中恰好有2天下雨的概率;
(2)從2011年開始到2019年該地區清明節當天降雨量(單位:![]() )如下表:(其中降雨量為0表示沒有下雨).
)如下表:(其中降雨量為0表示沒有下雨).
時間 | 2011年 | 2012年 | 2013年 | 2014年 | 2015年 | 2016年 | 2017年 | 2018年 | 2019年 |
年份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
降雨量 | 29 | 28 | 26 | 27 | 25 | 23 | 24 | 22 | 21 |
經研究表明:從2011年開始至2020年, 該地區清明節有降雨的年份的降雨量![]() 與年份
與年份![]() 成線性回歸,求回歸直線
成線性回歸,求回歸直線![]() ,并計算如果該地區2020年(
,并計算如果該地區2020年(![]() )清明節有降雨的話,降雨量為多少?(精確到0.01)
)清明節有降雨的話,降雨量為多少?(精確到0.01)
參考公式: .
.
參考數據:![]() ,
,![]() ,
,
![]() ,
,![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com