
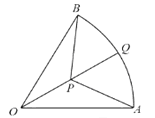
【題目】如圖,三個校區分別位于扇形OAB的三個頂點上,點Q是弧AB的中點,現欲在線段OQ上找一處開挖工作坑P(不與點O,Q重合),為小區鋪設三條地下電纜管線PO,PA,PB,已知OA=2千米,∠AOB=![]() ,記∠APQ=θrad,地下電纜管線的總長度為y千米.
,記∠APQ=θrad,地下電纜管線的總長度為y千米.
(1)將y表示成θ的函數,并寫出θ的范圍;
(2)請確定工作坑P的位置,使地下電纜管線的總長度最小.
【答案】(1)![]() (2)P與O的距離為
(2)P與O的距離為![]() 時,地下電纜管線的總長度最小
時,地下電纜管線的總長度最小
【解析】
(1)首先根據Q為弧AB的中點,得到知PA=PB,∠AOP=∠BOP=![]() ,利用正弦定理得到
,利用正弦定理得到 ,根據OA=2,得到PA=
,根據OA=2,得到PA=![]() ,OP=
,OP=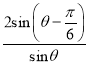 ,從而得到y=PA+PB+OP=2PA+OP=
,從而得到y=PA+PB+OP=2PA+OP=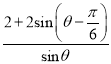 =
=![]() ,根據題意確定出
,根據題意確定出![]() ;
;
(2)對函數求導,令導數等于零,求得![]() ,確定出函數的單調區間,從而求得函數的最值.
,確定出函數的單調區間,從而求得函數的最值.
(1)因為Q為弧AB的中點,由對稱性,知PA=PB,∠AOP=∠BOP=![]() ,
,
又∠APO=![]() ,∠OAP=
,∠OAP=![]() ,
,
由正弦定理,得: ,又OA=2,
,又OA=2,
所以,PA=![]() ,OP=
,OP=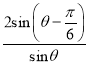 ,
,
所以,y=PA+PB+OP=2PA+OP=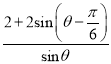 =
=![]() ,
,
∠APQ>∠AOP,所以,![]() ,∠OAQ=∠OQA=
,∠OAQ=∠OQA=![]() ,
,
所以,![]() ;
;
(2)令![]() ,
,![]()
![]() ,得:
,得:![]() ,
,
![]() 在
在![]() 上遞減,在
上遞減,在![]() 上遞增
上遞增
所以,當![]() ,即OP=
,即OP=![]() 時,
時,![]() 有唯一的極小值,
有唯一的極小值,
即是最小值:![]() =2
=2![]() ,
,
答:當工作坑P與O的距離為![]() 時,地下電纜管線的總長度最小.
時,地下電纜管線的總長度最小.


科目:高中數學 來源: 題型:
【題目】如圖,某公園內有一塊矩形綠地區域ABCD,已知AB=100米,BC=80米,以AD,BC為直徑的兩個半圓內種植花草,其它區域種值苗木. 現決定在綠地區域內修建由直路BN,MN和弧形路MD三部分組成的觀賞道路,其中直路MN與綠地區域邊界AB平行,直路為水泥路面,其工程造價為每米2a元,弧形路為鵝卵石路面,其工程造價為每米3a元,修建的總造價為W元. 設![]() .
.
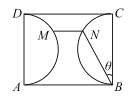
(1)求W關于![]() 的函數關系式;
的函數關系式;
(2)如何修建道路,可使修建的總造價最少?并求最少總造價.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某登山隊在山腳![]() 處測得山頂
處測得山頂![]() 的仰角為
的仰角為![]() ,沿傾斜角為
,沿傾斜角為![]() (其中
(其中![]() )的斜坡前進
)的斜坡前進![]() 后到達
后到達![]() 處,休息后繼續行駛
處,休息后繼續行駛![]() 到達山頂
到達山頂![]() .
.

(1)求山的高度![]() ;
;
(2)現山頂處有一塔![]() .從
.從![]() 到
到![]() 的登山途中,隊員在點
的登山途中,隊員在點![]() 處測得塔的視角為
處測得塔的視角為![]() .若點
.若點![]() 處高度
處高度![]() 為
為![]() ,則
,則![]() 為何值時,視角
為何值時,視角![]() 最大?
最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠為提高生產效率,開展技術創新活動,提出了完成某項生產任務的兩種新的生產方式.為比較兩種生產方式的效率,選取40名工人,將他們隨機分成兩組,每組20人,第一組工人用第一種生產方式,第二組工人用第二種生產方式.根據工人完成生產任務的工作時間(單位:min)繪制了如下莖葉圖:

(1)根據莖葉圖判斷哪種生產方式的效率更高?并說明理由;
(2)求40名工人完成生產任務所需時間的中位數![]() ,并將完成生產任務所需時間超過
,并將完成生產任務所需時間超過![]() 和不超過
和不超過![]() 的工人數填入下面的列聯表:
的工人數填入下面的列聯表:
超過 | 不超過 | |
第一種生產方式 | ||
第二種生產方式 |
(3)根據(2)中的列聯表,能否有99%的把握認為兩種生產方式的效率有差異?
附:![]() ,
,
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為實現有效利用扶貧資金,增加貧困村民的收入,扶貧工作組結合某貧困村水質優良的特點,決定利用扶貧資金從外地購買甲、乙、丙三種魚苗在魚塘中進行養殖試驗,試驗后選擇其中一種進行大面積養殖,已知魚苗甲的自然成活率為0.8.魚苗乙,丙的自然成活率均為0.9,且甲、乙、丙三種魚苗是否成活相互獨立.
(1)試驗時從甲、乙,丙三種魚苗中各取一尾,記自然成活的尾數為![]() ,求
,求![]() 的分布列和數學期望;
的分布列和數學期望;
(2)試驗后發現乙種魚苗較好,扶貧工作組決定購買![]() 尾乙種魚苗進行大面積養殖,為提高魚苗的成活率,工作組采取增氧措施,該措施實施對能夠自然成活的魚苗不產生影響.使不能自然成活的魚苗的成活率提高了50%.若每尾乙種魚苗最終成活后可獲利10元,不成活則虧損2元,且扶貧工作組的扶貧目標是獲利不低于37.6萬元,問需至少購買多少尾乙種魚苗?
尾乙種魚苗進行大面積養殖,為提高魚苗的成活率,工作組采取增氧措施,該措施實施對能夠自然成活的魚苗不產生影響.使不能自然成活的魚苗的成活率提高了50%.若每尾乙種魚苗最終成活后可獲利10元,不成活則虧損2元,且扶貧工作組的扶貧目標是獲利不低于37.6萬元,問需至少購買多少尾乙種魚苗?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于函數![]() ,若存在正常數
,若存在正常數![]() ,使得對任意的
,使得對任意的![]() ,都有
,都有![]() 成立,我們稱函數
成立,我們稱函數![]() 為“
為“![]() 同比不減函數”.
同比不減函數”.
(1)求證:對任意正常數![]() ,
,![]() 都不是“
都不是“![]() 同比不減函數”;
同比不減函數”;
(2)若函數![]() 是“
是“![]() 同比不減函數”,求
同比不減函數”,求![]() 的取值范圍;
的取值范圍;
(3)是否存在正常數![]() ,使得函數
,使得函數![]() 為“
為“![]() 同比不減函數”,若存在,求
同比不減函數”,若存在,求![]() 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com