
【題目】已知定義域為R的函數![]() 是奇函數
是奇函數
(1)求![]() 、
、![]() 的值;
的值;
(2)判斷![]() 的單調性(不需要證明),并寫出
的單調性(不需要證明),并寫出![]() 的值域;
的值域;
(3)若對任意的![]() ,不等式
,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
科目:高中數學 來源: 題型:
【題目】在研究塞卡病毒(Zika virus)某種疫苗的過程中,為了研究小白鼠連續接種該種疫苗后出現![]() 癥狀的情況,做接種試驗,試驗設計每天接種一次,連續接種3天為一個接種周期.已知小白鼠接種后當天出現
癥狀的情況,做接種試驗,試驗設計每天接種一次,連續接種3天為一個接種周期.已知小白鼠接種后當天出現![]() 癥狀的概率為
癥狀的概率為![]() ,假設每次接種后當天是否出現
,假設每次接種后當天是否出現![]() 癥狀與上次接種無關.
癥狀與上次接種無關.
(1)若出現![]() 癥狀即停止試驗,求試驗至多持續一個接種周期的概率;
癥狀即停止試驗,求試驗至多持續一個接種周期的概率;
(2)若在一個接種周期內出現2次貨3次![]() 癥狀,則這個接種周期結束后終止試驗,試驗至多持續3個周期,設接種試驗持續的接種周期數為
癥狀,則這個接種周期結束后終止試驗,試驗至多持續3個周期,設接種試驗持續的接種周期數為![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校為了解學生對食堂伙食的滿意程度,組織學生給食堂打分(分數為整數,滿分100分),從中隨機抽取一個容量為![]() 的樣本,發現所有數據均在
的樣本,發現所有數據均在![]() 內.現將這些分數分成以下
內.現將這些分數分成以下![]() 組:
組:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,并畫出了樣本的頻率分布直方圖,部分圖形如圖所示.觀察圖形,回答下列問題:
,并畫出了樣本的頻率分布直方圖,部分圖形如圖所示.觀察圖形,回答下列問題:
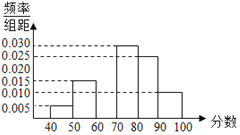
(1)算出第三組![]() 的頻數,并補全頻率分布直方圖;
的頻數,并補全頻率分布直方圖;
(2)請根據頻率分布直方圖,估計樣本的眾數和平均數,
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某基地蔬菜大棚采用水培、無土栽培方式種植各類蔬菜.過去50周的資料顯示,該地周光照量![]() (小時)都在30小時以上,其中不足50小時的周數有5周,不低于50小時且不超過70小時的周數有35周,超過70小時的周數有10周.根據統計,該基地的西紅柿增加量
(小時)都在30小時以上,其中不足50小時的周數有5周,不低于50小時且不超過70小時的周數有35周,超過70小時的周數有10周.根據統計,該基地的西紅柿增加量![]() (百斤)與使用某種液體肥料
(百斤)與使用某種液體肥料![]() (千克)之間對應數據為如圖所示的折線圖.
(千克)之間對應數據為如圖所示的折線圖.

(1)依據數據的折線圖,是否可用線性回歸模型擬合![]() 與
與![]() 的關系?請計算相關系數
的關系?請計算相關系數![]() 并加以說明(精確到0.01);(若
并加以說明(精確到0.01);(若![]() ,則線性相關程度很高,可用線性回歸模型擬合)
,則線性相關程度很高,可用線性回歸模型擬合)
(2)蔬菜大棚對光照要求較大,某光照控制儀商家為該基地提供了部分光照控制儀,但每周光照控制儀最多可運行臺數受周光照量![]() 限制,并有如表關系:
限制,并有如表關系:

若某臺光照控制儀運行,則該臺光照控制儀周利潤為3000元;若某臺光照控制儀未運行,則該臺光照控制儀周虧損1000元.以過去50周的周光照量的頻率作為周光照量發生的概率,商家欲使周總利潤的均值達到最大,應安裝光照控制儀多少臺?
附:相關系數公式 ,參考數據
,參考數據![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義在R上的函數f(x)滿足:如果對任意的x1,x2∈R,都有f(![]() )
)![]() ,則稱函數f(x)是R上的凹函數,已知二次函數f(x)=ax2+x(a∈R,a≠0)
,則稱函數f(x)是R上的凹函數,已知二次函數f(x)=ax2+x(a∈R,a≠0)
(1)當a=1,x∈[﹣2,2]時,求函數f(x)的值域;
(2)當a=1時,試判斷函數f(x)是否為凹函數,并說明理由;
(3)如果函數f(x)對任意的x∈[0,1]時,都有|f(x)|≤1,試求實數a的范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 是定義在
是定義在![]() 上的偶函數,當
上的偶函數,當![]() 時,
時, ![]() .
.
(1)直接寫出函數![]() 的增區間(不需要證明);
的增區間(不需要證明);
(2)求出函數![]() ,
, ![]() 的解析式;
的解析式;
(3)若函數![]() ,
, ![]() ,求函數
,求函數![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() 的定義域為
的定義域為![]() ,若存在閉區間
,若存在閉區間![]()
![]() ,使得
,使得![]() 函數滿足:(1)
函數滿足:(1)![]() 在
在![]() 上是單調函數;(2)
上是單調函數;(2)![]() 在
在![]() 上的值域是
上的值域是![]() ,則稱區間
,則稱區間![]() 是函數
是函數![]() 的“和諧區間”,下列結論錯誤的是( )
的“和諧區間”,下列結論錯誤的是( )
A.函數![]() 存在“和諧區間”
存在“和諧區間”
B.函數![]() 不存在“和諧區間”
不存在“和諧區間”
C.函數![]()
![]() 存在“和諧區間”
存在“和諧區間”
D.函數![]() (
(![]() ,
,![]() )不存在“和諧區間”
)不存在“和諧區間”
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】支付寶和微信支付是目前市場占有率較高的支付方式,某第三方調研機構對使用這兩種支付方式的人數作了對比.從全國隨機抽取了100個地區作為研究樣本,計算了各個地區樣本的使用人數,其頻率分布直方圖如圖.
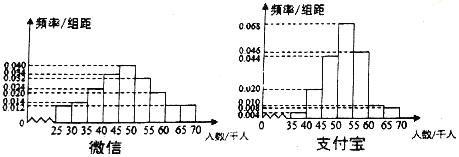
(1)記A表示事件“微信支付人數低于50千人”,估計A的概率;
(2)填寫下面列聯表,并根據列聯表判斷是否有99%的把握認為支付人數與支付方式有關;
支付人數<50千人 | 支付人數≥50千人 | 總計 | |
微信支付 | |||
支付寶支付 | |||
總計 |
(3)根據支付人數的頻率分布直方圖,對兩種支付方式的優劣進行比較.
附:
P(K2≥K) | 0.050 | 0.010 | 0.001 |
K | 3.841 | 6.635 | 10.828 |
K2=![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com