【題目】設
為常數）.
（1）當
時，求
的單調區間；
（2）若
在區間
的極大值、極小值各有一個，求實數
的取值范圍.
【答案】（1）單調遞增區間為
，單調遞減區間為
.（2）
【解析】試題分析：（1）先求導數，再根據導函數大于零得三角不等式，解得單調增區間；同理根據導函數小于零得三角不等式，解得單調減區間，注意單調區間不可用并集連接，（2）導函數
必有兩個不等的零點，利用導數分析導函數圖像得：先增后減再增，比較兩個端點及兩個極值點知，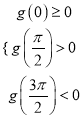 
，解不等式可得實數
的取值范圍.
試題解析：解：（1）當
時， 
，
令
，則
單調增；
令
，則
單調增，
所以
的單調遞增區間為
，單調遞減區間為
.
（2）設
，則
，
令
，則
，
令
，則
，
所以
的單調遞增區間為
，單調遞減區間為
.
故
在
處取得極大值，在
處取得極小值，
，
所以
①若
，則
在
上單調增，故
在
無極值，所以
；
②若
，則
在
內至多有一個極值點，從而
，
于是在區間
內
分別有極大值、極小值各一個，
則在
內無極值點，從而
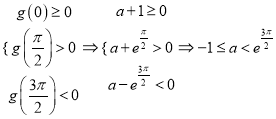，所以的取值范圍是
.
科目：高中數學 來源： 題型：
【題目】設{an}是一個公差不為零的等差數列，其前n項和為Sn ， 已知S9=90，且a1 ， a2 ， a4成等比數列．
（1）求數列{an}的通項公式；
（2）設bn= 
，求數列{bn}的前n項和Tn ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=sin（ωx+φ）其中ω＞0，|φ|＜ 
．
（1）若cos 
cosφ﹣sin 
sinφ=0．求φ的值；
（2）在（1）的條件下，若函數f（x）的圖象的相鄰兩條對稱軸之間的距離等于 
，求函數f（x）的解析式；并求最小正實數m，使得函數f（x）的圖象象左平移m個單位所對應的函數是偶函數．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】有下列四個說法：
①若函數f（x）=asinx+cosx（x∈R）的圖象關于直線x= 
對稱，則a= 
；
②已知向量 
=（1，2）， 
=（﹣2，m），若 與 的夾角為鈍角，則m＜1；
③當 
＜α＜ 
時，函數f（x）=sinx﹣logax有三個零點；
④函數f（x）=xsinx在[﹣ 
，0]上單調遞減，在[0， ]上單調遞增．
其中正確的是（填上所有正確說法的序號）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某市居民用水擬實行階梯水價，每人月用水量中不超過w立方米的部分按4元/立方米收費，超出w立方米的部分按10元/立方米收費，從該市隨機調查了10000位居民，獲得了他們某月的用水量數據，整理得到如圖頻率分布直方圖： 
（1）如果w為整數，那么根據此次調查，為使80%以上居民在該月的用水價格為4元/立方米，w至少定為多少？
（2）假設同組中的每個數據用該組區間的右端點值代替，當w=3時，估計該市居民該月的人均水費．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
（其中
， 
）.
（Ⅰ）當
時，若
對任意
恒成立，求實數
的取值范圍；
（Ⅱ）設函數
的圖象在兩點
、
處的切線分別為
、
，若
， 
，且
，求實數
的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）= 
cosx（sinx+cosx）． （Ⅰ）若0＜α＜ 
，且sinα= 
，求f（α）的值；
（Ⅱ）求函數f（x）的最小正周期及單調遞增區間．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
