
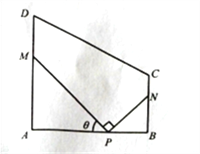
【題目】某地方政府要將一塊如圖所示的直角梯形ABCD空地改建為健身娛樂廣場.已知AD//BC, ![]() 百米,
百米, ![]() 百米,廣場入口P在AB上,且
百米,廣場入口P在AB上,且![]() ,根據(jù)規(guī)劃,過點P鋪設兩條相互垂直的筆直小路PM,PN(小路的寬度不計),點M,N分別在邊AD,BC上(包含端點),
,根據(jù)規(guī)劃,過點P鋪設兩條相互垂直的筆直小路PM,PN(小路的寬度不計),點M,N分別在邊AD,BC上(包含端點),![]() 區(qū)域擬建為跳舞健身廣場,
區(qū)域擬建為跳舞健身廣場, ![]() 區(qū)域擬建為兒童樂園,其它區(qū)域鋪設綠化草坪,設
區(qū)域擬建為兒童樂園,其它區(qū)域鋪設綠化草坪,設![]() .
.
(1)求綠化草坪面積的最大值;
(2)現(xiàn)擬將兩條小路PNM,PN進行不同風格的美化,PM小路的美化費用為每百米1萬元,PN小路的美化費用為每百米2萬元,試確定M,N的位置,使得小路PM,PN的美化總費用最低,并求出最小費用.
【答案】(1) 綠化草坪面積的最大值為 平方百米;(2)
平方百米;(2) ![]() 時總美化費用最低為4萬元.
時總美化費用最低為4萬元.
【解析】試題分析:(1)先求得![]()
![]() ,再利用均值不等式求得正解;(2)先求得
,再利用均值不等式求得正解;(2)先求得![]() ,
, ![]()
總美化費用為![]() ,再利用導數(shù)工具求得正解.
,再利用導數(shù)工具求得正解.
試題解析:(1)在![]() 中,
中, ![]() ,得
,得![]() ,
,
所以![]()
由![]() ,
,![]()
在![]() 中,
中, ![]() ,得
,得![]() ,
,
所以![]()
所以綠化草坪面積![]()
![]()
![]()
![]()
又因為![]()
當且當![]() ,即
,即![]() 。此時
。此時![]()
所以綠化草坪面積的最大值為 平方百米.
平方百米.
(2)方法一:在![]() 中,
中, ![]() ,得
,得![]() ,
,
由![]() ,
,![]()
在![]() 中,
中, ![]() ,得
,得![]() ,
,
所以總美化費用為![]()
![]()
![]()
令![]() 得
得![]() 列表如下
列表如下
|
|
|
|
|
|
| - | 0 | - | ||
|
| 單調(diào)遞減 |
| 單調(diào)遞增 |
|
所以當![]() 時,即
時,即![]() 時總美化費用最低為4萬元。
時總美化費用最低為4萬元。
方法二:在![]() 中,
中, ![]() ,得
,得![]() ,
,
由![]() ,
,![]()
在![]() 中,
中, ![]() ,得
,得![]() ,
,
所以總美化費用為![]()
![]()
令 得
得![]()
所以![]() ,
, 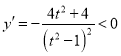
所以![]() 在
在 上是單調(diào)遞減
上是單調(diào)遞減
所以當![]() ,
, ![]() 時,即
時,即![]() 時總美化費用最低為4萬元。
時總美化費用最低為4萬元。


科目:高中數(shù)學 來源: 題型:
【題目】設數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,且對任意正整數(shù)
,且對任意正整數(shù)![]() ,滿足
,滿足![]() .
.
(1)求數(shù)列![]() 的通項公式.
的通項公式.
(2)設![]() ,求數(shù)列
,求數(shù)列![]() 的前
的前![]() 項和
項和![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,且對任意正整數(shù)
,且對任意正整數(shù)![]() ,滿足
,滿足![]() .
.
(1)求數(shù)列![]() 的通項公式.
的通項公式.
(2)設![]() ,求數(shù)列
,求數(shù)列![]() 的前
的前![]() 項和
項和![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某水果店購進某種水果的成本為![]() ,經(jīng)過市場調(diào)研發(fā)現(xiàn),這種水果在未來30天的銷售單價
,經(jīng)過市場調(diào)研發(fā)現(xiàn),這種水果在未來30天的銷售單價![]() 與時間
與時間![]() 之間的函數(shù)關(guān)系式為
之間的函數(shù)關(guān)系式為![]() ,銷售量
,銷售量![]() 與時間
與時間![]() 的函數(shù)關(guān)系式為
的函數(shù)關(guān)系式為![]() 。
。
(Ⅰ)該水果店哪一天的銷售利潤最大?最大利潤是多少?
(Ⅱ)為響應政府“精準扶貧”號召,該店決定每銷售![]() 水果就捐贈
水果就捐贈![]() 元給“精準扶貧”對象.欲使捐贈后不虧損,且利潤隨時間
元給“精準扶貧”對象.欲使捐贈后不虧損,且利潤隨時間![]()
![]() 的增大而增大,求捐贈額
的增大而增大,求捐贈額![]() 的值。
的值。
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() (
(![]() ,
,![]() 是自然對數(shù)的底數(shù)).
是自然對數(shù)的底數(shù)).
(1)若![]() 是
是![]() 上的單調(diào)遞增函數(shù),求實數(shù)
上的單調(diào)遞增函數(shù),求實數(shù)![]() 的取值范圍;
的取值范圍;
(2)當![]() 時,證明:函數(shù)
時,證明:函數(shù)![]() 有最小值,并求函數(shù)
有最小值,并求函數(shù)![]() 最小值的取值范圍.
最小值的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當![]() 時,利用函數(shù)單調(diào)性的定義判斷并證明
時,利用函數(shù)單調(diào)性的定義判斷并證明![]() 的單調(diào)性,并求其值域;
的單調(diào)性,并求其值域;
(2)若對任意![]() ,求實數(shù)
,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】試求下列函數(shù)的定義域與值域:
(1)f(x)=(x-1)2+1,x∈{-1,0,1,2,3};
(2)f(x)=(x-1)2+1;
(3)f(x)=![]() ;
;
(4)f(x)=x-![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)=x3+3x2-9x.
(I)求f(x)的單調(diào)區(qū)間;
(Ⅱ)若函數(shù)f(x)在區(qū)間[-4,c]上的最小值為-5,求c的取值范圍.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com