
【題目】如圖,已知直線![]() 交拋物線
交拋物線![]() 于
于![]() 、
、![]() 兩點(點
兩點(點![]() 在點
在點![]() 左側(cè)),過線段
左側(cè)),過線段![]() (兩端點除外)上的任意一點作直線
(兩端點除外)上的任意一點作直線![]() ,使得直線
,使得直線![]() 與拋物線
與拋物線![]() 在點
在點![]() 處的切線平行,設(shè)直線
處的切線平行,設(shè)直線![]() 與拋物線
與拋物線![]() 交于
交于![]() 、
、![]() 兩點.
兩點.
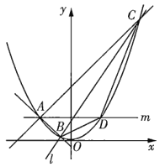
(1)記直線![]() 、
、![]() 的斜率分別為
的斜率分別為![]() 、
、![]() ,證明:
,證明:![]() ;
;
(2)若![]() ,求
,求![]() 的面積.
的面積.
【答案】(1)見解析;(2)![]() .
.
【解析】
(1)設(shè)![]() ,
,![]() ,
,![]() ,利用導(dǎo)數(shù)的幾何意義及直線的斜率公式求解;
,利用導(dǎo)數(shù)的幾何意義及直線的斜率公式求解;
(2)根據(jù)![]() 及
及![]() ,可得
,可得![]() ,表示出
,表示出![]() 、
、![]() ,再表示出
,再表示出![]() ,得到
,得到![]() ,設(shè)線段
,設(shè)線段![]() 的中點為
的中點為![]() ,求出
,求出![]() ,最后根據(jù)
,最后根據(jù)![]() 的中點
的中點![]() 與點
與點![]() 的連線平行于
的連線平行于![]() 軸,得
軸,得![]() ,從而得結(jié)果.
,從而得結(jié)果.
(1)由![]() 得,
得,![]() ,則
,則![]() .
.
設(shè)點![]() ,由導(dǎo)數(shù)的幾何意義知,直線
,由導(dǎo)數(shù)的幾何意義知,直線![]() 的斜率為
的斜率為![]() .
.
由題意知點![]() .設(shè)點
.設(shè)點![]() 、
、![]() ,
,
則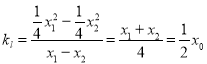 ,即
,即![]() .
.
因為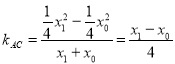 ,
,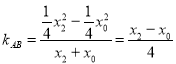 ,
,
所以![]() ;
;
(2)由![]() 且
且![]() 可知,
可知,![]() ,
,
不妨設(shè)點![]() 在
在![]() 上方,則
上方,則![]() ,
,
直線![]() 的方程為
的方程為![]() .
.
由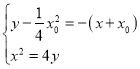 ,得點
,得點![]() 的坐標(biāo)為
的坐標(biāo)為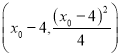 .
.
所以![]() ,同理可得
,同理可得![]() .
.
所以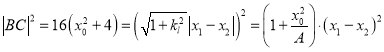 ,得
,得![]() .
.
設(shè)線段![]() 的中點為
的中點為![]() ,
,
則點![]() 的坐標(biāo)為
的坐標(biāo)為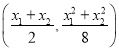 ,即
,即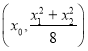 ,
,
連接![]() ,易知
,易知![]() ,
,
所以![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】A、B兩同學(xué)參加數(shù)學(xué)競賽培訓(xùn),在培訓(xùn)期間,他們參加了8次測驗,成績(單位:分)記錄如下:
A 71 62 72 76 63 70 85 83
B 73 84 75 73 7![]() 8
8![]() 76 85
76 85
B同學(xué)的成績不慎被墨跡污染(![]() ,
,![]() 分別用m,n表示).
分別用m,n表示).
(1)用莖葉圖表示這兩組數(shù)據(jù),現(xiàn)從A、B兩同學(xué)中選派一人去參加數(shù)學(xué)競賽,你認(rèn)為選派誰更好?請說明理由(不用計算);
(2)若B同學(xué)的平均分為78,方差![]() ,求m,n.
,求m,n.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)集![]() ,其中
,其中![]() ,且
,且![]() ,若對
,若對![]() ,
,![]() 與
與![]() 兩數(shù)中至少有一個屬于
兩數(shù)中至少有一個屬于![]() ,則稱數(shù)集
,則稱數(shù)集![]() 具有性質(zhì)
具有性質(zhì)![]() .
.
(1)分別判斷數(shù)集![]() 與數(shù)集
與數(shù)集![]() 是否具有性質(zhì)
是否具有性質(zhì)![]() ,說明理由;
,說明理由;
(2)已知數(shù)集![]() 具有性質(zhì)
具有性質(zhì)![]() ,判斷數(shù)列
,判斷數(shù)列![]() ,
,![]() ,…,
,…,![]() 是否為等差數(shù)列,若是等差數(shù)列,請證明;若不是,請說明理由.
是否為等差數(shù)列,若是等差數(shù)列,請證明;若不是,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() :
:![]() 的準(zhǔn)線經(jīng)過點
的準(zhǔn)線經(jīng)過點![]() ,過
,過![]() 的焦點
的焦點![]() 作兩條互相垂直的直線
作兩條互相垂直的直線![]() ,
,![]() ,直線
,直線![]() 與
與![]() 交于
交于![]() ,
,![]() 兩點,直線
兩點,直線![]() 與
與![]() 交于
交于![]() ,
,![]() 兩點,則下列結(jié)論正確的是( )
兩點,則下列結(jié)論正確的是( )
A.![]() B.
B.![]() 的最小值為16
的最小值為16
C.四邊形![]() 的面積的最小值為64D.若直線
的面積的最小值為64D.若直線![]() 的斜率為2,則
的斜率為2,則![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】點F2是雙曲線![]() 的右焦點,動點A在雙曲線左支上,直線l1:tx﹣y+t﹣2=0與直線l2:x+ty+2t﹣1=0的交點為B,則|AB|+|AF2|的最小值為( )
的右焦點,動點A在雙曲線左支上,直線l1:tx﹣y+t﹣2=0與直線l2:x+ty+2t﹣1=0的交點為B,則|AB|+|AF2|的最小值為( )
A.8B.![]() C.9D.
C.9D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在黨中央的英明領(lǐng)導(dǎo)下,在全國人民的堅定支持下,中國的抗擊“新型冠狀肺炎”戰(zhàn)役取得了階段性勝利,現(xiàn)在擺在我們大家面前的是有序且安全的復(fù)工復(fù)產(chǎn).某商場為了提振顧客的消費信心,對某中型商品實行分期付款方式銷售,根據(jù)以往資料統(tǒng)計,顧客購買該商品選擇分期付款的期數(shù)ξ的分布列為

其中0<a<1,0<b<1.
(1)求購買該商品的3位顧客中,恰有1位選擇分4期付款的概率;
(2)商場銷售一件該商品,若顧客選擇分4期付款,則商場獲得的利潤為2000元;若顧客選擇分5期付款,則商場獲得的利潤為2500元;若顧客選擇分6期付款,則商場獲得的利潤為3000元,假設(shè)該商場銷售兩件該商品所獲得的利潤為X(單位:元),
(i)設(shè)X=5500時的概率為m,求當(dāng)m取最大值時,利潤X的分布列和數(shù)學(xué)期望;
(ii)設(shè)某數(shù)列{xn}滿足x1=0.4,xn=a,2xn+1=b,若a<0.25,求n的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓C:![]() +
+![]() =1(a>b>0)的兩焦點之間的距離為2,兩條準(zhǔn)線間的距離為8,直線l:y=k(x-m)(m∈R)與橢圓交于P,Q兩點.
=1(a>b>0)的兩焦點之間的距離為2,兩條準(zhǔn)線間的距離為8,直線l:y=k(x-m)(m∈R)與橢圓交于P,Q兩點.
(1) 求橢圓C的方程;
(2) 設(shè)橢圓的左頂點為A,記直線AP,AQ的斜率分別為k1,k2.①若m=0,求k1k2的值;②若k1k2=-![]() ,求實數(shù)m的值.
,求實數(shù)m的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)數(shù)列![]() 的前n項和為
的前n項和為![]() ,
,![]()
(1)求證:數(shù)列![]() 是等比數(shù)列;
是等比數(shù)列;
(2)若![]() ,是否存在q的某些取值,使數(shù)列
,是否存在q的某些取值,使數(shù)列![]() 中某一項能表示為另外三項之和?若能求出q的全部取值集合,若不能說明理由.
中某一項能表示為另外三項之和?若能求出q的全部取值集合,若不能說明理由.
(3)若![]() ,是否存在
,是否存在![]() ,使數(shù)列
,使數(shù)列![]() 中,某一項可以表示為另外三項之和?若存在指出q的一個取值,若不存在,說明理由.
中,某一項可以表示為另外三項之和?若存在指出q的一個取值,若不存在,說明理由.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com