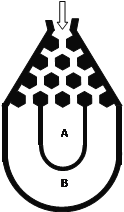
【題目】(本題滿分12分)將一個半徑適當?shù)男∏蚍湃肴鐖D所示的容器最上方的入口處,小球將自由下落.小球在下落過程中,將3次遇到黑色障礙物,最后落入
袋或
袋中.已知小球每次遇到黑色障礙物時向左、右兩邊下落的概率都是.
（Ⅰ）求小球落入袋中的概率
;
（Ⅱ）在容器入口處依次放入4個小球,記
為落入袋中小球的個數(shù),試求
的概率和的數(shù)學期望
.
名校課堂系列答案科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
為定義域R上的奇函數(shù)，且在R上是單調(diào)遞增函數(shù)，函數(shù)
，數(shù)列
為等差數(shù)列，且公差不為0，若
，則
( )
A. 45B. 15C. 10D. 0
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】某地擬規(guī)劃種植一批芍藥，為了美觀，將種植區(qū)域（區(qū)域I）設計成半徑為1km的扇形
，中心角
（
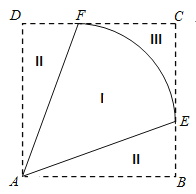
）.為方便觀賞，增加收入，在種植區(qū)域外圍規(guī)劃觀賞區(qū)（區(qū)域II）和休閑區(qū)（區(qū)域III），并將外圍區(qū)域按如圖所示的方案擴建成正方形
，其中點
，
分別在邊
和
上．已知種植區(qū)、觀賞區(qū)和休閑區(qū)每平方千米的年收入分別是10萬元、20萬元、20萬元.
（1）要使觀賞區(qū)的年收入不低于5萬元，求
的最大值；
（2）試問：當為多少時，年總收入最大？
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知三棱錐
的底面
是等邊三角形，點
在平面上的射影在
內(nèi)（不包括邊界），
.記
，
與底面所成角為
，
；二面角
，
的平面角為
，
，則，，，之間的大小關系等確定的是（）
A. 
B. 
C. 是最小角，是最大角D. 只能確定
，
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】在如圖所示的六面體中,面
是邊長為2的正方形,面
是直角梯形,
，
.
(1)求證:
平面
；
(2)若二面角
為60°,求直線
和平面所成角的正弦值.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】將一顆骰子先后拋擲2次，觀察向上的點數(shù)，事件A：“兩數(shù)之和為8”，事件B：“兩數(shù)之和是3的倍數(shù)”，事件C：“兩個數(shù)均為偶數(shù)”．
（I）寫出該試驗的基本事件
，并求事件A發(fā)生的概率；
（II）求事件B發(fā)生的概率；
（III）事件A與事件C至少有一個發(fā)生的概率．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】我國南北朝時期的數(shù)學家祖暅提出了計算幾何體體積的祖暅原理：“冪勢既同，則積不容異“．意思是兩個同高的幾何體，如果在等高處的截面積都相等，那么這兩個幾何體的體積相等．現(xiàn)有某幾何體和一個圓錐滿足祖暅原理的條件，若該圓錐的側面展開圖是半徑為3的圓的三分之一，則該幾何體的體積為（ ）
A.
πB.
πC.4
D.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知隨機變量X服從正態(tài)分布N（μ，σ2），且P（μ－2σ＜X＜μ＋2σ）＝0.954 4，P（μ－σ＜X＜μ＋σ）＝0.682 6.若μ＝4，σ＝1，則P（5＜X＜6）＝（ ）
A. 0.135 9 B. 0.135 8 C. 0.271 8 D. 0.271 6；
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
