
【題目】已知f(x)是R上的奇函數(shù),且x>0時,f(x)=x2-4x+3.
求:(1)f(x)的解析式.
(2)已知t>0,求函數(shù)f(x)在區(qū)間[t,t+1]上的最小值.
【答案】(1)f(x)=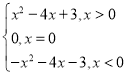 (2)
(2)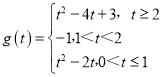
【解析】
(1)當(dāng)x<0時,-x>0,而f(x)=-f(-x)可求f(x)
(2)由題意可得函數(shù)f(x)[t,t+1]上f(x)=x2-4x+3=(x-2)2-1開口向上且關(guān)于x=2對稱
①當(dāng)t+1≤2時,函數(shù)f(x)在[t,t+1]上單調(diào)遞減,g(t)=f(t+1)
②當(dāng)t<2<t+1時即1<t<2時,對稱軸在區(qū)間內(nèi),g(t)=f(2)
③當(dāng)t≥2時,函數(shù)f(x)在[t,t+1]上單調(diào)遞增,g(t)=f(t)
(1)∵f(x)是奇函數(shù)
∴f(-x)=-f(x)對任意的x都成立, f(0)=0
又x>0時,f(x)=x2-4x+3.
∴x<0時,-x>0
∴f(x)=-f(-x)=-[(-x)2-4(-x)+3]=-x2-4x-3
∴f(x)=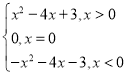
(2)∵t>0
∴當(dāng)x∈[t,t+1]時,f(x)=x2-4x+3=(x-2)2-1開口向上且關(guān)于x=2對稱
①當(dāng)t+1≤2時,函數(shù)f(x)在[t,t+1]上單調(diào)遞減
∴g(t)=f(t+1)=(t-1)2-1=t2-2t
②當(dāng)t<2<t+1時即1<t<2時,對稱軸在區(qū)間內(nèi)
∴g(t)=f(2)=-1
③當(dāng)t≥2時,函數(shù)f(x)在[t,t+1]上單調(diào)遞增
∴g(t)=f(t)=t2-4t+3
綜上所述,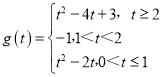



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】根據(jù)以往的經(jīng)驗(yàn),某建筑工程施工期間的降水量![]() (單位:
(單位:![]() )對工期的影響如下表:
)對工期的影響如下表:
降水量 |
|
|
|
|
工期延誤天數(shù) | 0 | 1 | 3 | 6 |
根據(jù)某氣象站的資料,某調(diào)查小組抄錄了該工程施工地某月前![]() 天的降水量的數(shù)據(jù),繪制得到降水量的折線圖,如下圖所示.
天的降水量的數(shù)據(jù),繪制得到降水量的折線圖,如下圖所示.

(1)求這![]() 天的平均降水量;
天的平均降水量;
(2)根據(jù)降水量的折線圖,分別估計該工程施工延誤天數(shù)![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當(dāng)![]() 時,
時,![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(2)證明:當(dāng)![]() 時,函數(shù)
時,函數(shù)![]() 有最小值,設(shè)
有最小值,設(shè)![]() 最小值為
最小值為![]() ,求函數(shù)
,求函數(shù)![]() 的值域.
的值域.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(Ⅰ)若函數(shù)![]() 在
在![]() 內(nèi)有極值,求實(shí)數(shù)
內(nèi)有極值,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(Ⅱ)在(Ⅰ)的條件下,對任意![]() ,
,![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)全集為R,集合A={x|-3<x<4},B={x|1≤x≤10}.
(1)求A∪B,A∩(RB);
(2)已知集合C={x|2a-1≤x≤a+1},若C∩A=C,求實(shí)數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)f(x)="xln" x–ax2+(2a–1)x,a![]() R.
R.
(Ⅰ)令g(x)=f'(x),求g(x)的單調(diào)區(qū)間;
(Ⅱ)已知f(x)在x=1處取得極大值.求實(shí)數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 且
且![]() 是
是![]() 的導(dǎo)函數(shù),則過曲線
的導(dǎo)函數(shù),則過曲線![]() 上一點(diǎn)
上一點(diǎn)![]() 的切線方程為
的切線方程為![]()
![]()
A. ![]() B.
B. ![]()
C. ![]() 或
或![]() D.
D. ![]() 或
或![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在三棱柱![]() 中,已知
中,已知![]() 側(cè)面
側(cè)面![]() ,
,![]() ,
,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 在棱
在棱![]() 上.
上.
(1)求![]() 的長,并證明
的長,并證明![]() 平面
平面![]() ;
;
(2)若![]() ,試確定
,試確定![]() 的值,使得
的值,使得![]() 到平面
到平面![]() 的距離為
的距離為![]() .
.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】程大位是明代著名數(shù)學(xué)家,他的《新編直指算法統(tǒng)宗》是中國歷史上一部影響巨大的著作,它問世后不久便風(fēng)行宇內(nèi),成為明清之際研習(xí)數(shù)學(xué)者必讀的教材,而且傳到朝鮮、日本及東南亞地區(qū),對推動漢字文化圈的數(shù)學(xué)發(fā)展起了重要的作用.卷八中第33問是:“今有三角果一垛,底闊每面七個,問該若干?”如圖是解決該問題的程序框圖,執(zhí)行該程序框圖,求得該垛果子的總數(shù)![]() 為( )
為( )

A. 120 B. 84 C. 56 D. 28
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com