
���}Ŀ����֪�E�A![]() ��
��![]() ��
��![]() �����c(di��n)
�����c(di��n)![]() ��
��![]() ������c(di��n)���c(di��n)
������c(di��n)���c(di��n)![]() ��
��![]() ��һ�c(di��n)���x����
��һ�c(di��n)���x����![]() .
.
��1����E�A![]() �ķ��̣�
�ķ��̣�
��2���O(sh��)�^(gu��)�c(di��n)![]() ��ֱ��
��ֱ��![]() �c
�c![]() ����һ��(g��)���c(di��n)��
����һ��(g��)���c(di��n)��![]() �������c(di��n)
�������c(di��n)![]() �����Ƿ����ֱ��
�����Ƿ����ֱ��![]() ��ʹ����
��ʹ����![]() ��ֱ���ĈA��(j��ng)�^(gu��)�c(di��n)
��ֱ���ĈA��(j��ng)�^(gu��)�c(di��n)![]() �������ڣ����ֱ��
�������ڣ����ֱ��![]() �ķ��̣��������ڣ��f(shu��)������.
�ķ��̣��������ڣ��f(shu��)������.
���𰸡���1��![]() ����2�����ڣ�
����2�����ڣ�![]()
��������
��1�����c(di��n)![]() ����E�AC�ķ��̣��ٽY(ji��)���x���ʣ��ɵ�a,b,c���P(gu��n)ϵ���ɵÙE�A�ķ�����
����E�AC�ķ��̣��ٽY(ji��)���x���ʣ��ɵ�a,b,c���P(gu��n)ϵ���ɵÙE�A�ķ�����
��2���O(sh��)��ֱ��![]() �ķ��̣�����E�A���\(y��n)���f�_(d��)����������c(di��n)
�ķ��̣�����E�A���\(y��n)���f�_(d��)����������c(di��n)![]() ������(bi��o)������
������(bi��o)������![]() �������ֱ���ķ���,Ҫע��z�(y��n)ֱ���Ƿ�͙E�A�Ѓɂ�(g��)���c(di��n)��
�������ֱ���ķ���,Ҫע��z�(y��n)ֱ���Ƿ�͙E�A�Ѓɂ�(g��)���c(di��n)��
��1�����}�ɵ�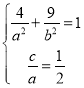 ��
��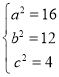 �����ԙE�A
�����ԙE�A![]() �ķ���
�ķ���![]()
��2�����}֪![]() ���O(sh��)
���O(sh��)![]() ��ֱ��
��ֱ��![]() ��б�ʴ����O(sh��)��
��б�ʴ����O(sh��)��![]() ��
��
�t![]() �c�E�A
�c�E�A![]() (li��n)����
(li��n)����![]()
![]() ��
��![]() ����
����![]() ��
��![]() ����
����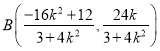
����![]() ��ֱ���ĈA��(j��ng)�^(gu��)�c(di��n)
��ֱ���ĈA��(j��ng)�^(gu��)�c(di��n)![]() ��
��
�t![]() ����
����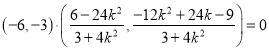 ��
��
����(ji��n)��![]() ����
����![]() �����
�����![]() ��
��![]()
��?y��n)?/span>![]() �c
�c![]() ���غϣ�����
���غϣ�����![]() ��.
��.
����ֱ��![]() �ķ��̞�
�ķ��̞�![]() .
.



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() .
.
��1��ԇӑՓ![]() �Ć��{(di��o)�ԣ�
�Ć��{(di��o)�ԣ�
��2����(d��ng)����(sh��)![]() ������(g��)��ͬ�����c(di��n)�r(sh��)��
������(g��)��ͬ�����c(di��n)�r(sh��)��![]() ��ȡֵ����ǡ����
��ȡֵ����ǡ����![]() ����
����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����С�}�M��13�֣�
�����ˆT���M(j��n)����վ���ij�(xi��ng)���и�ݗ��Σ�U(xi��n)���΄�(w��)��ÿ��ֻ��һ��(g��)���M(j��n)ȥ����ÿ��(g��)��ֻ��һ�Σ������r(sh��)�g�����^(gu��)10��犣������һ��(g��)��10��犃�(n��i)��������΄�(w��)�t������������һ��(g��)�ˣ��F(xi��n)��һ��ֻ�мס��ҡ�������(g��)�˿��ɣ���������������΄�(w��)�ĸ��ʷքe![]()
![]() �����O(sh��)
�����O(sh��)![]() ������ȣ��Ҽٶ������ܷ�����΄�(w��)���¼����(d��)��.
������ȣ��Ҽٶ������ܷ�����΄�(w��)���¼����(d��)��.
��1������������ȣ��Ҵ�֮��������������ˣ����΄�(w��)�ܱ���ɵĸ��ʣ�����׃?n��i)���(g��)�˱��ɳ����Ⱥ�����΄�(w��)�ܱ���ɵĸ����Ƿ�l(f��)��׃����
��2������ijָ��������ˣ��@����(g��)�˸���������΄�(w��)�ĸ������Ξ�![]() ������
������![]() ��
��![]() ��һ��(g��)���У��������ɳ��ˆT��(sh��)Ŀ
��һ��(g��)���У��������ɳ��ˆT��(sh��)Ŀ![]() �ķֲ��к;�ֵ����(sh��)��������
�ķֲ��к;�ֵ����(sh��)��������![]() ��
��
��3���ٶ�![]() ��ԇ���������ӵ��Ⱥ�����ɳ��ˆT����ʹ�����ɳ����ˆT��(sh��)Ŀ�ľ�ֵ����(sh��)���������_(d��)����С��
��ԇ���������ӵ��Ⱥ�����ɳ��ˆT����ʹ�����ɳ����ˆT��(sh��)Ŀ�ľ�ֵ����(sh��)���������_(d��)����С��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() .
.
��1����(d��ng)![]() �r(sh��)���O(sh��)
�r(sh��)���O(sh��)![]() ��
��![]() ��
��![]() �ăɂ�(g��)��ͬ�Oֵ�c(di��n)���C����
�ăɂ�(g��)��ͬ�Oֵ�c(di��n)���C����![]() ��
��
��2���O(sh��)![]() ��
��![]() ��
��![]() �ăɂ�(g��)��ͬ���c(di��n)���C����
�ăɂ�(g��)��ͬ���c(di��n)���C����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ�������{(di��o)�顰�p11�����M(f��i)���(d��ng)��r��ijУ�y(t��ng)Ӌ(j��)С�M�քe���L��![]() ��
��![]() �ɂ�(g��)С�^(q��)��20����ͥ��������(d��ng)�յ����M(f��i)�~��
�ɂ�(g��)С�^(q��)��20����ͥ��������(d��ng)�յ����M(f��i)�~��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �ֽM���քe���l�ʷֲ�ֱ���D�c�o�~�D�y(t��ng)Ӌ(j��)���£���λ��Ԫ����
�ֽM���քe���l�ʷֲ�ֱ���D�c�o�~�D�y(t��ng)Ӌ(j��)���£���λ��Ԫ����
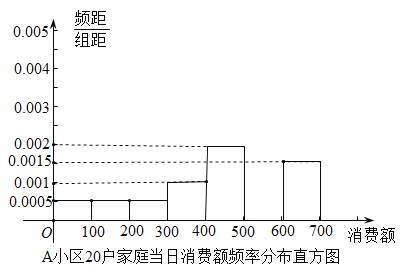
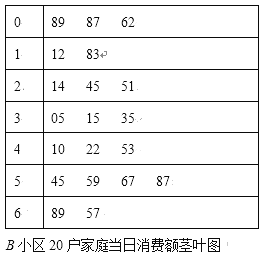
��1���քeӋ(j��)��ɂ�(g��)С�^(q��)�@20����ͥ��(d��ng)�����M(f��i)�~��![]() ���l�ʣ����a(b��)ȫ�l�ʷֲ�ֱ���D��
���l�ʣ����a(b��)ȫ�l�ʷֲ�ֱ���D��
��2���քe�ăɂ�(g��)С�^(q��)�S�C(j��)�xȡ1����ͥ�����@�ɑ���ͥ��(d��ng)�����M(f��i)�~��![]() �đ���(sh��)��1�r(sh��)�ĸ��ʣ��l�ʮ�(d��ng)������ʹ�ã���
�đ���(sh��)��1�r(sh��)�ĸ��ʣ��l�ʮ�(d��ng)������ʹ�ã���
��3���\(y��n)�����W(xu��)�y(t��ng)Ӌ(j��)֪�R(sh��)�������^�ɂ�(g��)С�^(q��)�Į�(d��ng)�վW(w��ng)ُ(g��u)���M(f��i)ˮƽ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
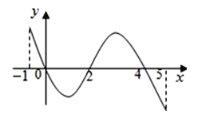
���}Ŀ����֪����(sh��)![]() �Ķ��x��?y��n)?/span>
�Ķ��x��?y��n)?/span>![]() ������(du��)��(y��ng)ֵ���±���
������(du��)��(y��ng)ֵ���±���
|
| 0 | 4 | 5 |
| 1 | 2 | 2 | 1 |
![]() ��(d��o)����(sh��)
�Č�(d��o)����(sh��)![]() �ĈD����D��ʾ���P(gu��n)��
�ĈD����D��ʾ���P(gu��n)��![]() �����}���_���ǣ� ��
�����}���_���ǣ� ��
A.����(sh��)![]() �����ں���(sh��)
�����ں���(sh��)
B.����(sh��)![]() ��
��![]() ���ǜp����(sh��)
���ǜp����(sh��)
C.����(sh��)![]() �����c(di��n)��(g��)��(sh��)���ܞ�0��1��2��3��4
�����c(di��n)��(g��)��(sh��)���ܞ�0��1��2��3��4
D.��(d��ng)![]() �r(sh��)������(sh��)
�r(sh��)������(sh��)![]() �� 4��(g��)���c(di��n)
�� 4��(g��)���c(di��n)
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
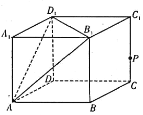
���}Ŀ�����c(di��n)![]() ���c(di��n)
���c(di��n)![]() ��ƽ��
��ƽ��![]() �ϵ���ͶӰ���tӛ
�ϵ���ͶӰ���tӛ![]() .��D�������L(zh��ng)��1�������w
.��D�������L(zh��ng)��1�������w![]() �У�ӛƽ��
�У�ӛƽ��![]() ��
��![]() ��ƽ��
��ƽ��![]() ��
��![]() ���c(di��n)
���c(di��n)![]() �Ǿ���
�Ǿ���![]() ��һ��(d��ng)�c(di��n)��
��һ��(d��ng)�c(di��n)��![]() .�o�������Ă�(g��)�Y(ji��)Փ��
.�o�������Ă�(g��)�Y(ji��)Փ��
��![]() ��
��![]() �����ģ�
�����ģ�
��![]() ��
��
�ۮ�(d��ng)![]() �r(sh��)��
�r(sh��)��![]() ƽ��
ƽ��![]() ��
��
�ܮ�(d��ng)�����F![]() ���w�e���r(sh��)�������F
���w�e���r(sh��)�������F![]() �����ı���e��
�����ı���e��![]() .
.
���У��������_�Y(ji��)Փ����̖(h��o)��________________.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����ֱ������(bi��o)ϵ![]() �У�ֱ��
�У�ֱ��![]() �ą���(sh��)���̞�
�ą���(sh��)���̞�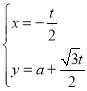 ��
��![]() ��t�酢��(sh��)��.������(bi��o)ԭ�c(di��n)��O�c(di��n)��
��t�酢��(sh��)��.������(bi��o)ԭ�c(di��n)��O�c(di��n)��![]() �S�����S��O�S�����O����(bi��o)ϵ������
�S�����S��O�S�����O����(bi��o)ϵ������![]() �ĘO����(bi��o)���̞�
�ĘO����(bi��o)���̞�![]() .
.
��1����ֱ������(bi��o)ϵ��ֱ��![]() �c����
�c����![]() ����ͨ���̣�
����ͨ���̣�
��2���O(sh��)ֱ��![]() �c����
�c����![]() �����c(di��n)
�����c(di��n)![]() ��
��![]() �����߿��غϣ�����
�����߿��غϣ�����![]() �S��
�S��![]() ����
����![]() ����
����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪�E�A![]() �����c(di��n)��
�����c(di��n)��![]() ��
��![]() �ǙE�A���P(gu��n)��ԭ�c(di��n)
�ǙE�A���P(gu��n)��ԭ�c(di��n)![]() ��(du��)�Q�ăɂ�(g��)��(d��ng)�c(di��n)����(d��ng)�c(di��n)
��(du��)�Q�ăɂ�(g��)��(d��ng)�c(di��n)����(d��ng)�c(di��n)![]() ������(bi��o)��
������(bi��o)��![]() �r(sh��)��
�r(sh��)��![]() �����L(zh��ng)ǡ��
�����L(zh��ng)ǡ��![]() ��
��
��1����E�A�ķ��̣�
��2���^(gu��)�c(di��n)![]() ��ֱ��
��ֱ��![]() ���E�A��
���E�A��![]() ���c(di��n)����
���c(di��n)����![]()
![]() ����
����![]() ��e��ȡֵ������
��e��ȡֵ������
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com