【題目】已知實數(shù)
及函數(shù)
（1）若
，求
的單調(diào)區(qū)間；
（2）設(shè)集合
，使
在
上恒成立的
的取值范圍記作集合
，求證： 
是
的真子集.
【答案】（1）
的單調(diào)遞減區(qū)間是
和
，增區(qū)間是
;（2）見解析.
【解析】試題分析：（1）
，所以
的單調(diào)遞減區(qū)間是
和
，增區(qū)間是
；（2）
，分類討論，得
是
的真子集。
試題解析：
（1）
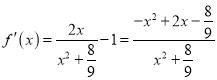
令
，得
或
，則
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
所以
的單調(diào)遞減區(qū)間是
和
，增區(qū)間是
（2）證明： 
時， 
的判別式
恒成立，所以
恒成立且有唯一的
值使
所以， 
時， 
在
上單調(diào)遞減.
所以
時， 
，所以
是
的子集；
時，令
，得
或
，則類比（1）可得在
上
的單調(diào)減區(qū)間是
和
，增區(qū)間是
取
，得
的單調(diào)減區(qū)間是
和
，增區(qū)間是
，所以在
上， 
時
取得最大值.
所以， 
時， 
恒成立，所以
，但
所以
是
的真子集.
科目：高中數(shù)學(xué) 來源： 題型：
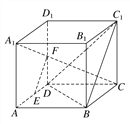
【題目】如圖，在正方體ABCD－A1B1C1D1中，E，F分別是AD，DD1的中點．
求證：(1)EF∥平面C1BD；
(2)A1C⊥平面C1BD.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】(2016·懷仁期中)已知命題
：x∈[－1,2]，函數(shù)f(x)＝x2－x的值大于0.若
∨
是真命題，則命題
可以是( )
A. x∈(－1,1)，使得cos x<
B. “－3<m<0”是“函數(shù)f(x)＝x＋log2x＋m在區(qū)間
上有零點”的必要不充分條件
C. 直線x＝
是曲線f(x)＝
的一條對稱軸
D. 若x∈(0,2)，則在曲線f(x)＝ex(x－2)上任意一點處的切線的斜率不小于－1
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】設(shè)函數(shù)f(x)＝emx＋x2－mx.
(1)證明：f(x)在(－∞，0)上單調(diào)遞減，在(0，＋∞)上單調(diào)遞增；
(2)若對于任意x1，x2∈[－1,1]，都有|f(x1)－f(x2)|≤e－1，求m的取值范圍．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知拋物線
的標準方程為
， 
為拋物線
上一動點， 
（
）為其對稱軸上一點，直線
與拋物線
的另一個交點為
．當
為拋物線
的焦點且直線
與其對稱軸垂直時， 
的面積為18．
（1）求拋物線
的標準方程；
（2）記
，若
值與
點位置無關(guān)，則稱此時的點
為“穩(wěn)定點”，試求出所有“穩(wěn)定點”，若沒有，請說明理由．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】我校為豐富師生課余活動，計劃在一塊直角三角形
的空地上修建一個占地面積為
（平方米）的
矩形健身場地，如圖，點
在
上，點
在
上，且
點在斜邊
上，已知
， 
米， 
米， 
.設(shè)矩形
健身場地每平方米的造價為
元，再把矩形
以外（陰影部分）鋪上草坪，每平方米的造價為
元（
為正常數(shù)）
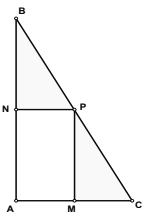
（1）試用
表示
，并求
的取值范圍；
（2）求總造價
關(guān)于面積
的函數(shù)
;
（3）如何選取
，使總造價
最低（不要求求出最低造價）
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
，
(1)若
,求函數(shù)
的極值及單調(diào)區(qū)間；
(2)若在區(qū)間
上至少存在一點
,使
成立,求實數(shù)
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
