
【題目】已知![]() 都是各項不為零的數(shù)列,且滿足
都是各項不為零的數(shù)列,且滿足![]() ,
,![]() ,其中
,其中![]() 是數(shù)列
是數(shù)列![]() 的前
的前![]() 項和,
項和,![]() 是公差為
是公差為![]() 的等差數(shù)列.
的等差數(shù)列.
(1)若數(shù)列![]() 的通項公式分別為
的通項公式分別為![]() ,求數(shù)列
,求數(shù)列![]() 的通項公式;
的通項公式;
(2)若![]() (
(![]() 是不為零的常數(shù)),求證:數(shù)列
是不為零的常數(shù)),求證:數(shù)列![]() 是等差數(shù)列;
是等差數(shù)列;
(3)若![]() (
(![]() 為常數(shù),
為常數(shù),![]() ),
),![]() (
(![]() ,
,![]() ),對任意
),對任意![]() ,
,![]() ,求出數(shù)列
,求出數(shù)列![]() 的最大項(用含
的最大項(用含![]() 式子表達(dá)).
式子表達(dá)).
【答案】(1)![]() ;(2)證明見解析;(3)
;(2)證明見解析;(3)![]() .
.
【解析】
(1)代入數(shù)據(jù)得到![]() ,根據(jù)通項和前
,根據(jù)通項和前![]() 項和關(guān)系并驗證得到答案.
項和關(guān)系并驗證得到答案.
(2)代入數(shù)據(jù)化簡得到![]() ,退項作減法得到
,退項作減法得到![]() (
(![]() ),再驗證
),再驗證![]() 的情況得到答案.
的情況得到答案.
(3)根據(jù)題意代數(shù)化簡得到![]() ,令
,令![]() ,證明
,證明![]() 時,
時,![]() 單調(diào)遞減,得到最大項.
單調(diào)遞減,得到最大項.
(1)因為![]() ,所以
,所以![]() ,
,
由![]() ,得
,得![]() ,
,
當(dāng)![]() 時,
時,![]() ,兩式作差,可得
,兩式作差,可得![]() ,
,
當(dāng)![]() 時,
時,![]() 滿足上式,則
滿足上式,則![]() .
.
(2)![]() ,當(dāng)
,當(dāng)![]() 時,
時,![]() ,
,
兩式相減得:![]() ,
,
即![]() ,即
,即![]() ,
,
又![]() ,所以
,所以![]() ,即
,即![]() ,
,
所以當(dāng)![]() 時,
時,![]() ,兩式相減得:
,兩式相減得:![]() ,
,
所以數(shù)列![]() 是從第二項起成公差為
是從第二項起成公差為![]() 的等差數(shù)列.
的等差數(shù)列.
又當(dāng)![]() 時,由
時,由![]() ,得
,得![]() ,
,
當(dāng)![]() 時,由
時,由![]() ,得
,得![]() ,
,
故數(shù)列![]() 是公差為
是公差為![]() 的等差數(shù)列.
的等差數(shù)列.
(3)當(dāng)![]() 時,
時,![]() ,
,
因為![]() ,所以
,所以![]() ,即
,即![]() ,
,
所以![]() ,即
,即![]() ,即
,即![]() ,
,
故從第二項起數(shù)列![]() 是等比數(shù)列,所以當(dāng)
是等比數(shù)列,所以當(dāng)![]() 時,
時,![]() ,
,
![]() ,
,
另外由已知條件可得![]() ,又
,又![]() ,
,
所以![]() ,因而
,因而![]() ,
,
令![]() ,則
,則![]() ,
,
故對任意的![]() 時,
時,![]() ,
,![]() 恒成立,
恒成立,
所以![]() 時,
時,![]() ,
,![]() 單調(diào)遞減,
單調(diào)遞減,![]() 中最大項為
中最大項為![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】四棱錐![]() 中,底面
中,底面![]() 是邊長為2的菱形,
是邊長為2的菱形,![]() ,
,![]() 為
為![]() 的中點,
的中點,![]() 平面
平面![]() ,
,![]() 與平面
與平面![]() 所成的角的正弦值為
所成的角的正弦值為![]() .
.

(1)在棱![]() 上求一點
上求一點![]() ,使
,使![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在三棱錐![]() 中,△ABC是等邊三角形,AB⊥AD,CB⊥CD,點P是AC的中點,記△BPD、△ABD的面積分別為
中,△ABC是等邊三角形,AB⊥AD,CB⊥CD,點P是AC的中點,記△BPD、△ABD的面積分別為![]() ,
,![]() ,二面角A-BD-C的大小為
,二面角A-BD-C的大小為![]() ,
,
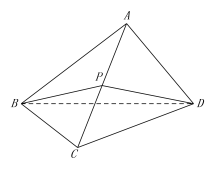
證明:(Ⅰ)平面ACD![]() 平面BDP;
平面BDP;
(Ⅱ)![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,曲線
中,曲線![]() 的方程是:
的方程是: ![]() ,以坐標(biāo)原點為極點,
,以坐標(biāo)原點為極點, ![]() 軸正半軸為極軸建立極坐標(biāo)系.
軸正半軸為極軸建立極坐標(biāo)系.
(1)求曲線![]() 的極坐標(biāo)方程;
的極坐標(biāo)方程;
(2)設(shè)過原點的直線![]() 與曲線
與曲線![]() 交于
交于![]() ,
, ![]() 兩點,且
兩點,且![]() ,求直線
,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】2018年元旦期間,某運動服裝專賣店舉辦了一次有獎促銷活動,消費每超過400元均可參加1次抽獎活動,抽獎方案有兩種,顧客只能選擇其中的一種.
方案一:顧客轉(zhuǎn)動十二等分且質(zhì)地均勻的圓形轉(zhuǎn)盤(如圖),轉(zhuǎn)盤停止轉(zhuǎn)動時指針指向哪個扇形區(qū)域,則顧客可直接獲得該區(qū)域?qū)?yīng)面額(單位:元)的現(xiàn)金優(yōu)惠,且允許顧客轉(zhuǎn)動3次.
方案二:顧客轉(zhuǎn)動十二等分且質(zhì)地均勻的圓形轉(zhuǎn)盤(如圖〕,轉(zhuǎn)盤停止轉(zhuǎn)動時指針若指向陰影部分,則未中獎,若指向白色區(qū)域,則顧客可直接獲得40元現(xiàn)金,且允許顧客轉(zhuǎn)動3次.

(1)若兩位顧客均獲得1次抽獎機會,且都選擇抽獎方案一,試求這兩位顧客均獲得180元現(xiàn)金優(yōu)惠的概率;
(2)若某顧客恰好獲得1次抽獎機會.
①試分別計算他選擇兩種抽獎方案最終獲得現(xiàn)金獎勵的數(shù)學(xué)期望;
②從概率的角度比較①中該顧客選擇哪一種抽獎方案更合算?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】選修4-4:坐標(biāo)系與參數(shù)方程
在平面直角坐標(biāo)系![]() 中,圓
中,圓![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)).以原點
為參數(shù)).以原點![]() 為極點,
為極點, ![]() 軸的正半軸為極軸,取相同的長度單位建立極坐標(biāo)系,直線
軸的正半軸為極軸,取相同的長度單位建立極坐標(biāo)系,直線![]() 的極坐標(biāo)方程是
的極坐標(biāo)方程是![]() .
.
(1)求直線![]() 的直角坐標(biāo)方程與圓
的直角坐標(biāo)方程與圓![]() 的普通方程;
的普通方程;
(2)點![]() 為直線
為直線![]() 上的一動點,過點
上的一動點,過點![]() 作直線
作直線![]() 與圓
與圓![]() 相切于點
相切于點![]() ,求四邊形
,求四邊形![]() 的面積的最小值.
的面積的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,在直角梯形![]() 中,
中,![]() ,
,![]() 、
、![]() 分別是
分別是![]() 、
、![]() 上的點,
上的點,![]() ,且
,且![]() (如圖①).將四邊形
(如圖①).將四邊形![]() 沿
沿![]() 折起,連接
折起,連接![]() 、
、![]() 、
、![]() (如圖②).在折起的過程中,則下列表述:
(如圖②).在折起的過程中,則下列表述:

①![]() 平面
平面![]() ;
;
②四點![]() 、
、![]() 、
、![]() 、
、![]() 可能共面;
可能共面;
③若![]() ,則平面
,則平面![]() 平面
平面![]() ;
;
④平面![]() 與平面
與平面![]() 可能垂直.其中正確的是__________.
可能垂直.其中正確的是__________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】王老師的班上有四個體育健將甲、乙、丙、丁,他們都特別擅長短跑,在某次運動會上,他們四人要組成一個![]() 米接力隊,王老師要安排他們四個人的出場順序,以下是他們四人的對話:
米接力隊,王老師要安排他們四個人的出場順序,以下是他們四人的對話:
甲:我不跑第一棒和第二棒;乙:我不跑第一棒和第四棒;
丙:我也不跑第一棒和第四棒;丁:如果乙不跑第二棒,我就不跑第一棒;
王老師聽了他們四人的對話,安排了一種合理的出場順序,滿足了他們的所有要求, 據(jù)此我們可以斷定,在王老師安排的出場順序中,跑第三棒的人是( )
A. 甲 B. 乙 C. 丙 D. 丁
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】科學(xué)研究證實,二氧化碳等溫空氣體的排放(簡稱碳排放)對全球氣候和生態(tài)環(huán)境產(chǎn)生了負(fù)面影響,環(huán)境部門對![]() 市每年的碳排放總量規(guī)定不能超過
市每年的碳排放總量規(guī)定不能超過![]() 萬噸,否則將采取緊急限排措施.已知
萬噸,否則將采取緊急限排措施.已知![]() 市
市![]() 年的碳排放總量為
年的碳排放總量為![]() 萬噸,通過技術(shù)改造和倡導(dǎo)低碳生活等措施,此后每年的碳排放量比上一年的碳排放總量減少
萬噸,通過技術(shù)改造和倡導(dǎo)低碳生活等措施,此后每年的碳排放量比上一年的碳排放總量減少![]() .同時,因經(jīng)濟發(fā)展和人口增加等因素,每年又新增加碳排放量
.同時,因經(jīng)濟發(fā)展和人口增加等因素,每年又新增加碳排放量![]() 萬噸
萬噸![]() .
.
(1)求![]() 市
市![]() 年的碳排放總量(用含
年的碳排放總量(用含![]() 的式子表示);
的式子表示);
(2)若![]() 市永遠(yuǎn)不需要采取緊急限排措施,求
市永遠(yuǎn)不需要采取緊急限排措施,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com