
【題目】正三棱柱ABC﹣A1B1C1底面△ABC的邊長為3,此三棱柱的外接球的半徑為 ![]() ,則異面直線AB1與BC1所成角的余弦值為 .
,則異面直線AB1與BC1所成角的余弦值為 .
【答案】![]()
【解析】解:設(shè)三棱柱外接球的球心為O,球半徑為r, 三棱柱的底面三角形ABC的中心為D,如圖,
∵正三棱柱ABC﹣A1B1C1底面△ABC的邊長為3,此三棱柱的外接球的半徑為 ![]() ,
,
∴OA= ![]() ,AD=
,AD= ![]() =
= ![]() ,
,
∴OD= ![]() =2,∴AA1=4,
=2,∴AA1=4,
以A為原點(diǎn),以過A在平面ABC中作AC的垂線為x軸,以AC為y軸,AA1為z軸,
建立空間直角坐標(biāo)系,
A(0,0,0),B( ![]() ,
, ![]() ,0),
,0),
B1( ![]() ,
, ![]() ,4),C1(0,3,4),
,4),C1(0,3,4),![]() =(
=( ![]() ,
, ![]() ,4),
,4), ![]() =(﹣
=(﹣ ![]() ,
, ![]() ,4),
,4),
設(shè)異面直線AB1與BC1所成角為θ,
則cosθ=  =
= ![]() =
= ![]() .
.
∴異面直線AB1與BC1所成角的余弦值為 ![]() .
.
所以答案是: ![]() .
.
【考點(diǎn)精析】掌握異面直線及其所成的角是解答本題的根本,需要知道異面直線所成角的求法:1、平移法:在異面直線中的一條直線中選擇一特殊點(diǎn),作另一條的平行線;2、補(bǔ)形法:把空間圖形補(bǔ)成熟悉的或完整的幾何體,如正方體、平行六面體、長方體等,其目的在于容易發(fā)現(xiàn)兩條異面直線間的關(guān)系.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線的頂點(diǎn)在原點(diǎn),過點(diǎn)A(-4,4)且焦點(diǎn)在x軸.
(1)求拋物線方程;
(2)直線l過定點(diǎn)B(-1,0)與該拋物線相交所得弦長為8,求直線l的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】等差數(shù)列{an}的前n項(xiàng)和為Sn , 已知a2=7,a3為整數(shù),且Sn的最大值為S5 .
(1)求{an}的通項(xiàng)公式;
(2)設(shè)bn= ![]() ,求數(shù)列{bn}的前n項(xiàng)和Tn .
,求數(shù)列{bn}的前n項(xiàng)和Tn .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知美國蘋果公司生產(chǎn)某款iphone手機(jī)的年固定成本為40萬美元,每生產(chǎn)1只還需另投入16美元.設(shè)蘋果公司一年內(nèi)共生產(chǎn)該款iphone手機(jī)x萬只并全部銷售完,每萬只的銷售收入為R(x)萬美元,且R(x)= 
(1)寫出年利潤W(萬元)關(guān)于年產(chǎn)量x(萬只)的函數(shù)解析式;
(2)當(dāng)年產(chǎn)量為多少萬只時,蘋果公司在該款手機(jī)的生產(chǎn)中所獲得的利潤最大?并求出最大利潤.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,已知圓
中,已知圓![]() 的半徑為2,圓心在
的半徑為2,圓心在![]() 軸的正半軸上,且與直線
軸的正半軸上,且與直線![]() 相切.
相切.
(1)求圓![]() 的方程。
的方程。
(2)在圓![]() 上,是否存在點(diǎn)
上,是否存在點(diǎn)![]() ,使得直線
,使得直線![]() 與圓
與圓![]() 相交于不同的兩點(diǎn)
相交于不同的兩點(diǎn)![]() ,且△
,且△![]() 的面積最大?若存在,求出點(diǎn)
的面積最大?若存在,求出點(diǎn)![]() 的坐標(biāo)及對應(yīng)的△
的坐標(biāo)及對應(yīng)的△![]() 的面積;若不存在,請說明理由.
的面積;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖是2017年第一季度五省GDP情況圖,則下列陳述中不正確的是( )
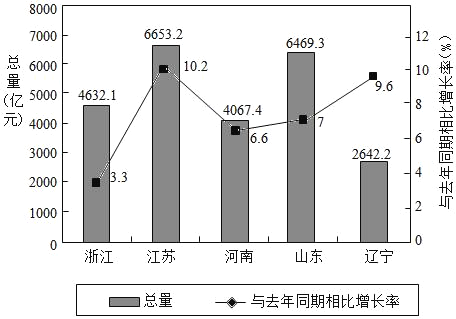
A. 2017年第一季度![]() 總量和增速由高到低排位均居同一位的省只有1個
總量和增速由高到低排位均居同一位的省只有1個
B. 與去年同期相比,2017年第一季度五個省的![]() 總量均實(shí)現(xiàn)了增長
總量均實(shí)現(xiàn)了增長
C. 去年同期河南省的![]() 總量不超過4000億元
總量不超過4000億元
D. 2017年第一季度![]() 增速由高到低排位第5的是浙江省
增速由高到低排位第5的是浙江省
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列四個命題中:①“等邊三角形的三個內(nèi)角均為60°”的逆命題;
②“若![]() ,則方程
,則方程![]() 有實(shí)根”的逆否命題;
有實(shí)根”的逆否命題;
③“全等三角形的面積相等”的否命題;
④“若![]() ,則
,則![]() ”的否命題.
”的否命題.
其中真命題的個數(shù)是( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在△ABC中,角A,B,C的對邊分別為a,b,c,且滿足 ![]() =
= ![]() .
.
(Ⅰ)求角A的大小;
(Ⅱ)若a=2 ![]() ,求△ABC面積的最大值.
,求△ABC面積的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)f(x)=2x﹣a,g(x)=x+2.
(1)當(dāng)a=1時,求不等式f(x)+f(﹣x)≤g(x)的解集;
(2)求證: ![]() 中至少有一個不小于
中至少有一個不小于 ![]() .
.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com