【題目】已知函數(shù)
為R上的偶函數(shù)，當(dāng)
時
當(dāng)
時，
且
對
恒成立，函數(shù)
的一個周期內(nèi)的圖像與函數(shù)
的圖像恰好有兩個公共點，則
（ ）
A. 
B. 
C. 
D. 
【答案】A
【解析】
先
對
恒成立得
恒成立，由當(dāng)
時，
；當(dāng)
時，
，得函數(shù)
在
上單調(diào)遞減，在
單調(diào)遞增，由函數(shù)
為R上的偶函數(shù)，且
時，
，可得函數(shù)在上單調(diào)遞減，在單調(diào)遞增，且圖像關(guān)于y軸對稱，最小值為
，又因為
的一個周期內(nèi)的圖像與函數(shù)的圖像恰好有兩個公共點，且
最大值為1，所以的最小正周期
，且過點
，然后可求出解析式.
解：因為對恒成立，且
的最大值為1
所以恒成立
又當(dāng)時，；當(dāng)時，
所以函數(shù)在上單調(diào)遞減，在單調(diào)遞增
又因為函數(shù)為R上的偶函數(shù)，且時，
所以函數(shù)在上單調(diào)遞減，在單調(diào)遞增，且圖像關(guān)于y軸對稱
所以函數(shù)的最小值為
因為函數(shù)最大值為1
且與的圖像恰好有兩個公共點，
則這兩個公共點必在
和
處
所以函數(shù)的最小正周期，所以
又過點，即
,所以
所以
故選：A
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知
，
是橢圓
的左、右焦點，橢圓
過點
.
（1）求橢圓的方程；
（2）過點
的直線
（不過坐標(biāo)原點）與橢圓交于
，
兩點，且點在
軸上方，點在軸下方，若
，求直線的斜率.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】隨著互聯(lián)網(wǎng)的興起，越來越多的人選擇網(wǎng)上購物.某購物平臺為了吸引顧客，提升銷售額，每年雙十一都會進行某種商品的促銷活動.該商品促銷活動規(guī)則如下：①“價由客定”，即所有參與該商品促銷活動的人進行網(wǎng)絡(luò)報價，每個人并不知曉其他人的報價，也不知道參與該商品促銷活動的總?cè)藬?shù)；②報價時間截止后，系統(tǒng)根據(jù)當(dāng)年雙十一該商品數(shù)量配額，按照參與該商品促銷活動人員的報價從高到低分配名額；③每人限購一件，且參與人員分配到名額時必須購買.某位顧客擬參加2019雙十一該商品促銷活動，他為了預(yù)測該商品最低成交價，根據(jù)該購物平臺的公告，統(tǒng)計了最近5年雙十一參與該商品促銷活動的人數(shù)（見下表）
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份編號t | 1 | 2 | 3 | 4 | 5 |
參與人數(shù)（百萬人） | 0.5 | 0.6 | 1 | 1.4 | 1.7 |
（1）由收集數(shù)據(jù)的散點圖發(fā)現(xiàn)，可用線性回歸模型模擬擬合參與人數(shù)
（百萬人）與年份編號
之間的相關(guān)關(guān)系.請用最小二乘法求關(guān)于的線性回歸方程：
，并預(yù)測2019年雙十一參與該商品促銷活動的人數(shù)；
（2）該購物平臺調(diào)研部門對2000位擬參與2019年雙十一該商品促銷活動人員的報價價格進行了一個抽樣調(diào)查，得到如下的一份頻數(shù)表：
報價區(qū)間(千元) |
|
|
|
|
|
|
頻數(shù) | 200 | 600 | 600 | 300 | 200 | 100 |
①求這2000為參與人員報價
的平均值
和樣本方差
（同一區(qū)間的報價可用該價格區(qū)間的中點值代替）；
②假設(shè)所有參與該商品促銷活動人員的報價可視為服從正態(tài)分布
，且
與
可分別由①中所求的樣本平均值和樣本方差估值.若預(yù)計2019年雙十一該商品最終銷售量為317400，請你合理預(yù)測（需說明理由）該商品的最低成交價.
參考公式即數(shù)據(jù)（i）回歸方程：，其中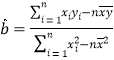
，
（ii）
（iii）若隨機變量
服從正態(tài)分布，則
，
，
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】從1到9的九個數(shù)字中取三個偶數(shù)四個奇數(shù)，試問：
（1）能組成多少個沒有重復(fù)數(shù)字的七位數(shù)？
（2）在（1）中的七位數(shù)中三個偶數(shù)排在一起的有幾個？
（3）在（1）中的七位數(shù)中，偶數(shù)排在一起、奇數(shù)也排在一起的有幾個？
（4）在（1）中任意兩偶然都不相鄰的七位數(shù)有幾個？
（答題要求：先列式，后計算 , 結(jié)果用具體數(shù)字表示．）
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
，其中
R．
（1）如果曲線
在x＝1處的切線斜率為1，求實數(shù)的值；
（2）若函數(shù)
的極小值不超過
，求實數(shù)的最小值；
（3）對任意
[1，2]，總存在
[4，8]，使得
＝
成立，求實數(shù)的取值范圍．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，正方形ADEF與梯形ABCD所在平面互相垂直，
，
，點M是EC的中點．
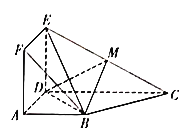
(1)求證:平面ADEF
平面BDE.
(2)求二面角
的余弦值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】設(shè)某大學(xué)的女生體重y（單位：kg）與身高x（單位：cm）具有線性相關(guān)關(guān)系，根據(jù)一組樣本數(shù)據(jù)（xi，yi）（i=1，2，…，n），用最小二乘法建立的回歸方程為
=0.85x-85.71，則下列結(jié)論中不正確的是
A. y與x具有正的線性相關(guān)關(guān)系
B. 回歸直線過樣本點的中心（
，
）
C. 若該大學(xué)某女生身高增加1cm，則其體重約增加0.85kg
D. 若該大學(xué)某女生身高為170cm，則可斷定其體重比為58.79kg
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知橢圓
的中心在坐標(biāo)原點，焦點在
軸上，左頂點為
，左焦點為
，點
在橢圓
上，直線
與橢圓
交于
， 
兩點，直線
， 
分別與
軸交于點
， 
．
（Ⅰ）求橢圓
的方程；
（Ⅱ）以
為直徑的圓是否經(jīng)過定點？若經(jīng)過，求出定點的坐標(biāo)；若不經(jīng)過，請說明理由．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】記
表示
，
中的最大值，如
．已知函數(shù)
，
．
（1）設(shè)
，求函數(shù)
在
上零點的個數(shù)；
（2）試探討是否存在實數(shù)
，使得
對
恒成立？若存在，求
的取值范圍；若不存在，說明理由．
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
