
【題目】已知函數f(x)=2sin(x+ ![]() )cosx.
)cosx.
(Ⅰ)求f(x)的值域;
(Ⅱ)設△ABC的內角A、B、C所對的邊分別為a、b、c,已知A為銳角,f(A)= ![]() ,b=2,c=3,求cos(A﹣B)的值.
,b=2,c=3,求cos(A﹣B)的值.
【答案】解:(Ⅰ)∵函數f(x)=2sin(x+ ![]() )cosx =(sinx+
)cosx =(sinx+ ![]() cosx)cosx=
cosx)cosx= ![]() sin2x+
sin2x+ ![]()
![]() =sin(2x+
=sin(2x+ ![]() )+
)+ ![]() ,
,
所以函數f(x)的值域是[ ![]() ,
, ![]() ].
].
(Ⅱ)△ABC中,∵A為銳角,f(A)=sin(2A+ ![]() )+
)+ ![]() =
= ![]() ,
,
∴sin(2A+ ![]() )=0,∴2A+
)=0,∴2A+ ![]() =π,∴A=
=π,∴A= ![]() .
.
又 b=2,c=3,由余弦定理可得a2=b2+c2﹣2bccosA=4+9﹣12cos ![]() =7,∴a=
=7,∴a= ![]() .
.
由 ![]() =
= ![]() ,得sinB=
,得sinB= ![]() ,又b<a,從而B<A,∴cosB=
,又b<a,從而B<A,∴cosB= ![]() =
= ![]() .
.
∴cos(A﹣B)=cosAcosB+sinAsinB= ![]() +
+ ![]() =
= ![]()
【解析】(Ⅰ)利用簡單的三角恒等變換化簡函數的解析式,再利用正弦函數的值域,得出結論.(Ⅱ)△ABC中,由f(A)= ![]() ,求得A的值,利用正弦定理、余弦定理求得a、sinB的值,可得cosB的值,從而求得cos(A﹣B)=cosAcosB+sinAsinB 的值.
,求得A的值,利用正弦定理、余弦定理求得a、sinB的值,可得cosB的值,從而求得cos(A﹣B)=cosAcosB+sinAsinB 的值.


科目:高中數學 來源: 題型:
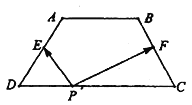
【題目】如圖,梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 和
和![]() 分別為
分別為![]() 與
與![]() 的中點,對于常數
的中點,對于常數![]() ,在梯形
,在梯形![]() 的四條邊上恰好有8個不同的點
的四條邊上恰好有8個不同的點![]() ,使得
,使得![]() 成立,則實數
成立,則實數![]() 的取值范圍是( )
的取值范圍是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設Sn是數列{an}的前n項和,已知a1=2,an+1=Sn+2.
(1)求數列{an}的通項公式.
(2)令bn=(2n﹣1)an , 求數列{bn}的前n項和Tn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】電視傳媒公司為了解某地區電視觀眾對某類體育節目的收視情況,隨機抽取了100名觀眾進行調查.下面是根據調查結果繪制的觀眾日均收看該體育節目時間的頻率分布直方圖:
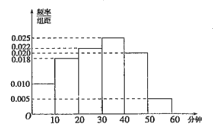
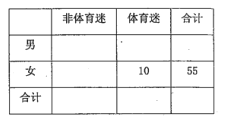
將日均收看該體育節目時間不低于40分鐘的觀眾稱為“體育迷”.
(1)根據已知條件完成上面的![]() 列聯表,若按
列聯表,若按![]() 的可靠性要求,并據此資料,你是否認為“體育迷”與性別有關?
的可靠性要求,并據此資料,你是否認為“體育迷”與性別有關?
(2)將上述調查所得到的頻率視為概率.現在從該地區大量電視觀眾中,采用隨機抽樣方法每次抽取1名觀眾,抽取3次,記被抽取的3名觀眾中的“體育迷”人數為![]() .若每次抽取的結果是相互獨立的,求
.若每次抽取的結果是相互獨立的,求![]() 分布列,期望
分布列,期望![]() 和方差
和方差![]() .
.
附: 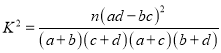

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校從高一年級期末考試的學生中抽出60名學生,其成績(均為整數)的頻率分布直方圖如圖所示: 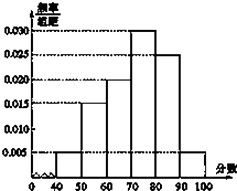
(1)依據頻率分布直方圖,估計這次考試的及格率(60分及以上為及格)和平均分;
(2)已知在[90,100]段的學生的成績都不相同,且都在94分以上,現用簡單隨機抽樣方法,從95,96,97,98,99,100這6個數中任取2個數,求這2個數恰好是兩個學生的成績的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩位學生參加數學競賽培訓,現分別從他們在培訓期間參加的若干次預賽成績中隨機抽取8次,記錄如下:
甲 | 82 | 81 | 79 | 78 | 95 | 88 | 93 | 84 |
乙 | 92 | 95 | 80 | 75 | 83 | 80 | 90 | 85 |
(1)用莖葉圖表示這兩組數據;
(2)現要從中選派一人參加數學競賽,從統計學的角度(在平均數、方差或標準差中選兩個)考慮,你認為選派哪位學生參加合適?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市居民用水擬實行階梯水價,每人月用水量中不超過w立方米的部分按4元/立方米收費,超出w立方米的部分按10元/立方米收費,從該市隨機調查了10000位居民,獲得了他們某月的用水量數據,整理得到如圖頻率分布直方圖: 
(1)如果w為整數,那么根據此次調查,為使80%以上居民在該月的用水價格為4元/立方米,w至少定為多少?
(2)假設同組中的每個數據用該組區間的右端點值代替,當w=3時,估計該市居民該月的人均水費.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com