
【題目】設函數(shù)![]()
(1)討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(2)若![]() 有兩個極值點
有兩個極值點![]() ,記過點
,記過點![]() 的直線的斜率為
的直線的斜率為![]() ,問:是否存在實數(shù)
,問:是否存在實數(shù)![]() ,使得
,使得![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
【答案】(1)見解析(2)不存在![]() ,使得
,使得![]() .
.
【解析】【試題分析】(1)先對函數(shù)![]() 求導,再運用導數(shù)與函數(shù)的單調(diào)性的關系分析討論函數(shù)
求導,再運用導數(shù)與函數(shù)的單調(diào)性的關系分析討論函數(shù)![]() 的符號,進而運用分類整合思想對實數(shù)
的符號,進而運用分類整合思想對實數(shù)![]() 進行分
進行分![]() 三類進行討論并判定其單調(diào)性,求出單調(diào)區(qū)間;(2)先假設滿足題設條件的參數(shù)
三類進行討論并判定其單調(diào)性,求出單調(diào)區(qū)間;(2)先假設滿足題設條件的參數(shù)![]() 存在,再借助題設條件,推得
存在,再借助題設條件,推得![]() ,即
,即![]() ,亦即
,亦即![]()
進而轉(zhuǎn)化為判定函數(shù)![]() 在
在![]() 上是單調(diào)遞增的問題,然后借助導數(shù)與函數(shù)單調(diào)性的關系運用反證法進行分析推證,從而作出判斷:
上是單調(diào)遞增的問題,然后借助導數(shù)與函數(shù)單調(diào)性的關系運用反證法進行分析推證,從而作出判斷:
解:(Ⅰ) ![]() 定義域為
定義域為![]() ,
,
![]() ,
,
令![]() ,
,
①當![]() 時,
時, ![]() ,
, ![]() ,故
,故![]() 在
在![]() 上單調(diào)遞增,
上單調(diào)遞增,
②當![]() 時,
時, ![]() ,
, ![]() 的兩根都小于零,在
的兩根都小于零,在![]() 上,
上, ![]() ,
,
故![]() 在
在![]() 上單調(diào)遞增,
上單調(diào)遞增,
③當![]() 時,
時, ![]() ,
, ![]() 的兩根為
的兩根為![]() ,
,
當![]() 時,
時, ![]() ;當
;當![]() 時,
時, ![]() ;當
;當![]() 時,
時, ![]() ;
;
故![]() 分別在
分別在![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 上單調(diào)遞減.
上單調(diào)遞減.
(Ⅱ)由(Ⅰ)知, ![]() ,
,
因為![]() .
.
所以![]() ,
,
又由(1)知, ![]() ,于是
,于是![]() ,
,
若存在![]() ,使得
,使得![]() ,則
,則![]() ,即
,即![]() ,
,
亦即![]() (
(![]() )
)
再由(Ⅰ)知,函數(shù)![]() 在
在![]() 上單調(diào)遞增,
上單調(diào)遞增,
而![]() ,所以
,所以![]() ,這與(
,這與(![]() )式矛盾,
)式矛盾,
故不存在![]() ,使得
,使得![]() .
.


 奪冠訓練單元期末沖刺100分系列答案
奪冠訓練單元期末沖刺100分系列答案 新思維小冠軍100分作業(yè)本系列答案
新思維小冠軍100分作業(yè)本系列答案科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系xoy中,已知圓C1:(x+3)2+(y﹣1)2=4和圓C2:(x﹣4)2+(y﹣5)2=4
(1)若直線l過點A(4,0),且被圓C1截得的弦長為2 ![]() ,求直線l的方程
,求直線l的方程
(2)設P為平面上的點,滿足:存在過點P的無窮多對互相垂直的直線l1和l2 , 它們分別與圓C1和C2相交,且直線l1被圓C1截得的弦長與直線l2被圓C2截得的弦長相等,求所有滿足條件的點P的坐標.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]()
(Ⅰ)若![]() ,求函數(shù)
,求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅱ)若對任意![]() 都有
都有![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍;
的取值范圍;
(Ⅲ)設函數(shù)![]() ,求證:
,求證:![]()
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】中國歷法推測遵循以測為輔、以算為主的原則.例如《周髀算經(jīng)》和《易經(jīng)》里對二十四節(jié)氣的晷影長的記錄中,冬至和夏至的晷影長是實測得到的,其他節(jié)氣的晷影長則是按照等差數(shù)列的規(guī)律計算得出的.下表為《周髀算經(jīng)》對二十四節(jié)氣晷影長的記錄,其中![]() 寸表示115寸
寸表示115寸![]() 分(1寸=10分).
分(1寸=10分).
節(jié)氣 | 冬至 | 小寒(大雪) | 大寒(小雪) | 立春(立冬) | 雨水(霜降) | 驚蟄(寒露) | 春分(秋分) |
晷影長(寸) | 135 |
|
|
|
|
| 75.5 |
節(jié)氣 | 清明(白露) | 谷雨(處暑) | 立夏(立秋) | 小滿(大暑) | 芒種(小暑) | 夏至 | |
晷影長(寸) |
|
|
|
|
| 16.0 |
已知《易知》中記錄的冬至晷影長為130.0寸,夏至晷影長為14.8寸,那么《易經(jīng)》中所記錄的驚蟄的晷影長應為__________寸.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】為了解某社區(qū)居民的家庭年收入與年支出的關系,相關部門隨機調(diào)查了該社區(qū)5戶家庭,得到如表統(tǒng)計數(shù)據(jù)表:
收入x(萬元) | 8.2 | 8.6 | 10.0 | 11.3 | 11.9 |
支出y(萬元) | 6.2 | 7.5 | 8.0 | 8.5 | 9.8 |
(1)根據(jù)上表可得回歸直線方程 ![]() =
= ![]() x+
x+ ![]() ,其中
,其中 ![]() =0.76,
=0.76, ![]() =
= ![]() ﹣
﹣ ![]()
![]() ,據(jù)此估計,該社區(qū)一戶年收入為15萬元的家庭年支出為多少?
,據(jù)此估計,該社區(qū)一戶年收入為15萬元的家庭年支出為多少?
(2)若從這5個家庭中隨機抽選2個家庭進行訪談,求抽到家庭的年收入恰好一個不超過10萬元,另一個超過11萬元的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知向量 ![]() =(sinθ,﹣2)與
=(sinθ,﹣2)與 ![]() =(1,cosθ)互相垂直,其中θ∈(0,
=(1,cosθ)互相垂直,其中θ∈(0, ![]() ).
).
(Ⅰ)求sinθ和cosθ的值;
(Ⅱ)若sin(θ﹣φ)= ![]() ,0<φ<
,0<φ< ![]() ,求cosφ的值.
,求cosφ的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,已知OPQ是半徑為1,圓心角為 ![]() 的扇形,C是扇形弧上的動點,ABCD是扇形的內(nèi)接矩形.記∠COP=α,則矩形ABCD的面積最大是 .
的扇形,C是扇形弧上的動點,ABCD是扇形的內(nèi)接矩形.記∠COP=α,則矩形ABCD的面積最大是 . 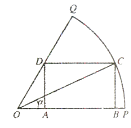
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設O為坐標原點,動點M在橢圓C![]() 上,過M作x軸的垂線,垂足為N,點P滿足
上,過M作x軸的垂線,垂足為N,點P滿足![]()
(1) 求點P的軌跡方程;
(2)設點![]() 在直線x=-3上,且
在直線x=-3上,且![]() .證明過點P且垂直于OQ的直線l過C的左焦點F.
.證明過點P且垂直于OQ的直線l過C的左焦點F.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com