
(14分)(2011•天津)已知函數f(x)=4x3+3tx2﹣6t2x+t﹣1,x∈R,其中t∈R.
(Ⅰ)當t=1時,求曲線y=f(x)在點(0,f(0))處的切線方程;
(Ⅱ)當t≠0時,求f(x)的單調區間;
(Ⅲ)證明:對任意的t∈(0,+∞),f(x)在區間(0,1)內均存在零點.
(Ⅰ)y=﹣6x
(Ⅱ)(1)若t<0,則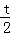 <﹣t,∴f(x)的單調增區間是(﹣∞,
<﹣t,∴f(x)的單調增區間是(﹣∞,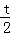 ),(﹣t,+∞);f(x)的單調減區間是(
),(﹣t,+∞);f(x)的單調減區間是(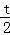 ,﹣t)
,﹣t)
(2)若t>0,則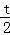 >﹣t,∴f(x)的單調增區間是(﹣∞,﹣t),(
>﹣t,∴f(x)的單調增區間是(﹣∞,﹣t),(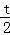 ,+∞);f(x)的單調減區間是(﹣t,
,+∞);f(x)的單調減區間是(﹣t,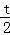 )
)
(Ⅲ)見解析
解析試題分析:(I)當t=1時,求出函數f(x),利用導數的幾何意義求出x=0處的切線的斜率,利用點斜式求出切線方程;
(II)根據f'(0)=0,解得x=﹣t或x=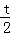 ,討論t的正負,在函數的定義域內解不等式fˊ(x)>0和fˊ(x)<0求出單調區間即可;
,討論t的正負,在函數的定義域內解不等式fˊ(x)>0和fˊ(x)<0求出單調區間即可;
(III)根據函數的單調性分兩種情況討論,當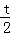 ≥1與當0<
≥1與當0<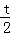 <1時,研究函數的單調性,然后根據區間端點的符號進行判定對任意t∈(0,2),f(x)在區間(0,1)內均存在零點從而得到結論.
<1時,研究函數的單調性,然后根據區間端點的符號進行判定對任意t∈(0,2),f(x)在區間(0,1)內均存在零點從而得到結論.
解:(I)當t=1時,f(x)=4x3+3x2﹣6x,f(0)=0
f'(x)=12x2+6x﹣6,f'(0)=﹣6,所以曲線y=f(x)在點(0,f(0))處的切線方程為y=﹣6x.
(II)解:f'(x)=12x2+6tx﹣6t2,f'(0)=0,解得x=﹣t或x=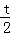
∵t≠0,以下分兩種情況討論:
(1)若t<0,則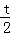 <﹣t,∴f(x)的單調增區間是(﹣∞,
<﹣t,∴f(x)的單調增區間是(﹣∞,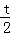 ),(﹣t,+∞);f(x)的單調減區間是(
),(﹣t,+∞);f(x)的單調減區間是(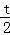 ,﹣t)
,﹣t)
(2)若t>0,則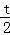 >﹣t,∴f(x)的單調增區間是(﹣∞,﹣t),(
>﹣t,∴f(x)的單調增區間是(﹣∞,﹣t),(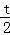 ,+∞);f(x)的單調減區間是(﹣t,
,+∞);f(x)的單調減區間是(﹣t,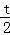 )
)
(III)證明:由(II)可知,當t>0時,f(x)在(0,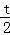 )內單調遞減,在(
)內單調遞減,在(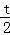 ,+∞)內單調遞增,以下分兩種情況討論:
,+∞)內單調遞增,以下分兩種情況討論:
(1)當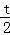 ≥1,即t≥2時,f(x)在(0,1)內單調遞減.
≥1,即t≥2時,f(x)在(0,1)內單調遞減.
f(0)=t﹣1>0,f(1)=﹣6t2+4t+3≤﹣13<0
所以對于任意t∈[2,+∞),f(x)在區間(0,1)內均存在零點.
(2)當0<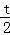 <1,即0<t<2時,f(x)在(0,
<1,即0<t<2時,f(x)在(0,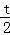 )內單調遞減,在(
)內單調遞減,在(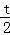 ,1)內單調遞增
,1)內單調遞增
若t∈(0,1],f(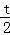 )=
)=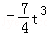 +t﹣1≤
+t﹣1≤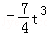 <0,
<0,
f(1)=)=﹣6t2+4t+3≥﹣2t+3>0
所以f(x)在(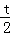 ,1)內存在零點.
,1)內存在零點.
若t∈(1,2),f(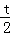 )=
)=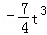 +t﹣1<
+t﹣1<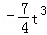 +1<0,
+1<0,
f(0)=t﹣1>0∴f(x)在(0,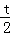 )內存在零點.
)內存在零點.
所以,對任意t∈(0,2),f(x)在區間(0,1)內均存在零點.
綜上,對于任意t∈(0,+∞),f(x)在區間(0,1)內均存在零點.
點評:本題主要考查了導數的幾何意義,利用導數研究函數的單調性、曲線的切線方程、函數零點、解不等式等基礎知識,考查了計算能力和分類討論的思想.


 開心蛙狀元測試卷系列答案
開心蛙狀元測試卷系列答案科目:高中數學 來源: 題型:解答題
已知函數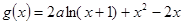 .
.
(1)當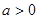 時,討論函數
時,討論函數 的單調性;
的單調性;
(2)當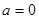 時,在函數
時,在函數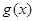 圖象上取不同兩點A、B,設線段AB的中點為
圖象上取不同兩點A、B,設線段AB的中點為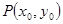 ,試探究函數
,試探究函數 在Q
在Q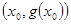 點處的切線與直線AB的位置關系?
點處的切線與直線AB的位置關系?
(3)試判斷當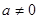 時
時 圖象是否存在不同的兩點A、B具有(2)問中所得出的結論.
圖象是否存在不同的兩點A、B具有(2)問中所得出的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(13分)(2011•重慶)設f(x)=x3+ax2+bx+1的導數f′(x)滿足f′(1)=2a,f′(2)=﹣b,其中常數a,b∈R.
(Ⅰ)求曲線y=f(x)在點(1,f(1))處的切線方程.
(Ⅱ)設g(x)=f′(x)e﹣x.求函數g(x)的極值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com