
【題目】已知函數(shù) ![]() 在
在 ![]() 處有極值
處有極值 ![]() .
.
(1)求 ![]() ,
, ![]() 的值;
的值;
(2)判斷函數(shù) ![]() 的單調(diào)性并求出單調(diào)區(qū)間.
的單調(diào)性并求出單調(diào)區(qū)間.
【答案】
(1)解:f′(x)=2ax+ ![]() ,
,
又f(x)在x=1處有極值 ![]() ,
,
∴ 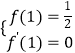 ,即
,即 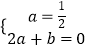
解得a= ![]() ,b=-1.
,b=-1.
經(jīng)檢驗(yàn)得a= ![]() ,b=-1函數(shù)f(x)=ax2+blnx在x=1處有極值
,b=-1函數(shù)f(x)=ax2+blnx在x=1處有極值 ![]() .
.
(2)解:由(1)可知f(x)= ![]() x2-lnx,其定義域是(0,+∞),且f′(x)=x-
x2-lnx,其定義域是(0,+∞),且f′(x)=x- ![]() =
= ![]() .
.
令f′(x)=0,解得x=1或x=-1(舍去).
當(dāng)x變化時(shí),f′(x),f(x)的變化情況如下表:
x | (0,1) | 1 | (1,+∞) |
f′(x) | - | 0 | + |
f(x) | 極小值 |
所以函數(shù)y=f(x)的單調(diào)減區(qū)間是(0,1),單調(diào)增區(qū)間是(1,+∞).
【解析】(1)根據(jù)題意求出導(dǎo)函數(shù)利用極值的定義列出關(guān)于a和b的函數(shù)式即可求出結(jié)果。(2)利用導(dǎo)函數(shù)以及極值的情況求出函數(shù)的單調(diào)性。



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】隨著國(guó)家二孩政策的全面放開(kāi),為了調(diào)查一線城市和非一線城市的二孩生育意愿,某機(jī)構(gòu)用簡(jiǎn)單隨機(jī)抽樣方法從不同地區(qū)調(diào)查了100位育齡婦女,結(jié)果如表.
非一線 | 一線 | 總計(jì) | |
愿生 | 45 | 20 | 65 |
不愿生 | 13 | 22 | 35 |
總計(jì) | 58 | 42 | 100 |
附表:
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
由K2= ![]() 算得,K2=
算得,K2= ![]() ≈9.616參照附表,得到的正確結(jié)論是( )
≈9.616參照附表,得到的正確結(jié)論是( )
A.在犯錯(cuò)誤的概率不超過(guò)0.1%的前提下,認(rèn)為“生育意愿與城市級(jí)別有關(guān)”
B.在犯錯(cuò)誤的概率不超過(guò)0.1%的前提下,認(rèn)為“生育意愿與城市級(jí)別無(wú)關(guān)”
C.有99%以上的把握認(rèn)為“生育意愿與城市級(jí)別有關(guān)”
D.有99%以上的把握認(rèn)為“生育意愿與城市級(jí)別無(wú)關(guān)”
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】下列說(shuō)法錯(cuò)誤的是( )
A.命題“若 ![]() ,則
,則 ![]() ”的逆否命題為:“若
”的逆否命題為:“若 ![]() ,則
,則 ![]() ”
”
B.“ ![]() ”是“
”是“ ![]() ”的充分不必要條件
”的充分不必要條件
C.若 ![]() 且
且 ![]() 為假命題,則
為假命題,則 ![]() 、
、 ![]() 均為假命題
均為假命題
D.命題 ![]() :“
:“ ![]() ,使得
,使得 ![]() ”,則
”,則 ![]() :“
:“ ![]() ,均有
,均有 ![]() ”
”
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)有兩個(gè)命題, ![]() :關(guān)于
:關(guān)于 ![]() 的不等式
的不等式 ![]() (
( ![]() ,且
,且 ![]() )的解集是
)的解集是 ![]() ;
; ![]() :函數(shù)
:函數(shù) ![]() 的定義域?yàn)?
的定義域?yàn)?![]() .如果
.如果 ![]() 為真命題,
為真命題, ![]() 為假命題,求實(shí)數(shù)
為假命題,求實(shí)數(shù) ![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】下列命題正確的個(gè)數(shù)為( )
①“x∈R都有x2≥0”的否定是“x0∈R使得x02≤0”;
②“x≠3”是“|x|≠3”成立的充分條件;
③命題“若m≤ ![]() ,則方程mx2+2x+2=0有實(shí)數(shù)根”的否命題為真命題.
,則方程mx2+2x+2=0有實(shí)數(shù)根”的否命題為真命題.
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)雙曲線 ![]() (a>0,b>0)的左焦點(diǎn)為F1 , 左頂點(diǎn)為A,過(guò)F1作x軸的垂線交雙曲線于P、Q兩點(diǎn),過(guò)P作PM垂直QA于M,過(guò)Q作QN垂直PA于N,設(shè)PM與QN的交點(diǎn)為B,若B到直線PQ的距離大于a+
(a>0,b>0)的左焦點(diǎn)為F1 , 左頂點(diǎn)為A,過(guò)F1作x軸的垂線交雙曲線于P、Q兩點(diǎn),過(guò)P作PM垂直QA于M,過(guò)Q作QN垂直PA于N,設(shè)PM與QN的交點(diǎn)為B,若B到直線PQ的距離大于a+ ![]() ,則該雙曲線的離心率取值范圍是( )
,則該雙曲線的離心率取值范圍是( )
A.(1﹣ ![]() )
)
B.( ![]() ,+∞)
,+∞)
C.(1,2 ![]() )
)
D.(2 ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù) ![]() 是自然對(duì)數(shù)的底數(shù),
是自然對(duì)數(shù)的底數(shù), ![]() .
.
(1)求函數(shù) ![]() 的單調(diào)遞增區(qū)間;
的單調(diào)遞增區(qū)間;
(2)若 ![]() 為整數(shù),
為整數(shù), ![]() ,且當(dāng)
,且當(dāng) ![]() 時(shí),
時(shí), ![]() 恒成立,其中
恒成立,其中 ![]() 為
為 ![]() 的導(dǎo)函數(shù),求
的導(dǎo)函數(shù),求 ![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】甲、乙兩地相距![]() ,汽車從甲地行駛到乙地,速度不得超過(guò)
,汽車從甲地行駛到乙地,速度不得超過(guò)![]() ,已知汽車每小時(shí)的運(yùn)輸成本(以元為單位)由可變部分和固定部分組成:可變部分與速度
,已知汽車每小時(shí)的運(yùn)輸成本(以元為單位)由可變部分和固定部分組成:可變部分與速度![]() (
(![]() )的平方成正比,比例系數(shù)為
)的平方成正比,比例系數(shù)為![]() ,固定部分為
,固定部分為![]() 元,
元,
(1)把全程運(yùn)輸成本![]() (元)表示為速度
(元)表示為速度![]() (
(![]() )的函數(shù),指出定義域;
)的函數(shù),指出定義域;
(2)為了使全程運(yùn)輸成本最小,汽車應(yīng)以多大速度行駛?
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com