
【題目】記無(wú)窮數(shù)列![]() 的前n項(xiàng)中最大值為
的前n項(xiàng)中最大值為![]() ,最小值為
,最小值為![]() ,令
,令![]() ,數(shù)列
,數(shù)列![]() 的前n項(xiàng)和為
的前n項(xiàng)和為![]() ,數(shù)列
,數(shù)列![]() 的前n項(xiàng)和為
的前n項(xiàng)和為![]() .
.
(1)若數(shù)列![]() 是首項(xiàng)為2,公比為2的等比數(shù)列,求
是首項(xiàng)為2,公比為2的等比數(shù)列,求![]() ;
;
(2)若數(shù)列![]() 是等差數(shù)列,試問(wèn)數(shù)列
是等差數(shù)列,試問(wèn)數(shù)列![]() 是否也一定是等差數(shù)列?若是,請(qǐng)證明;若不是,請(qǐng)舉例說(shuō)明;
是否也一定是等差數(shù)列?若是,請(qǐng)證明;若不是,請(qǐng)舉例說(shuō)明;
(3)若![]() ,求
,求![]() .
.
【答案】(1)![]() ;(2)見(jiàn)解析;(3)
;(2)見(jiàn)解析;(3)![]() ,
,![]()
【解析】
(1)由題意求得![]() 和
和![]() ,即得
,即得![]() ,利用等比數(shù)列求和公式可得結(jié)果.
,利用等比數(shù)列求和公式可得結(jié)果.
(2)若“數(shù)列{bn}是等差數(shù)列”,設(shè)其公差為d′,bn+1﹣bn![]() d′,根據(jù)定義,Mn+1≥Mn,mn+1≤mn,至少有一個(gè)取等號(hào),當(dāng)d′>0時(shí),Mn+1>Mn,an+1=Mn+1>Mn≥an,即數(shù)列{an}為增數(shù)列,則Mn=an,mn=a1,進(jìn)而得出.同理可得d′<0時(shí),“數(shù)列{an}是等差數(shù)列”;當(dāng)d′=0時(shí),Mn+1=Mn,且mn+1=mn,故{an}為常數(shù)列,是等差數(shù)列.
d′,根據(jù)定義,Mn+1≥Mn,mn+1≤mn,至少有一個(gè)取等號(hào),當(dāng)d′>0時(shí),Mn+1>Mn,an+1=Mn+1>Mn≥an,即數(shù)列{an}為增數(shù)列,則Mn=an,mn=a1,進(jìn)而得出.同理可得d′<0時(shí),“數(shù)列{an}是等差數(shù)列”;當(dāng)d′=0時(shí),Mn+1=Mn,且mn+1=mn,故{an}為常數(shù)列,是等差數(shù)列.
(3)由題意可得![]() ,根據(jù)定義可以分析得到當(dāng)
,根據(jù)定義可以分析得到當(dāng)![]() 時(shí),
時(shí),![]() ,即得
,即得![]() ;同理可得
;同理可得![]() 時(shí),
時(shí),![]() .,
.,
所以當(dāng)![]() 時(shí),
時(shí),![]() ,
,![]() 得到
得到![]() 可得
可得![]() ,求得
,求得
![]() ;當(dāng)
;當(dāng)![]() 時(shí),
時(shí),![]() 得到
得到![]() ,求得
,求得![]() ,分段寫(xiě)出結(jié)果即可.
,分段寫(xiě)出結(jié)果即可.
(1)∵數(shù)列![]() 是首項(xiàng)為2,公比為2的等比數(shù)列,∴
是首項(xiàng)為2,公比為2的等比數(shù)列,∴![]() ,∴
,∴![]() ,
,![]()
則![]() ,∴
,∴![]()
(2)若數(shù)列![]() 是等差數(shù)列,設(shè)其公差為
是等差數(shù)列,設(shè)其公差為![]()
∵![]()
![]()
根據(jù)![]() ,
,![]() 的定義,有以下結(jié)論:
的定義,有以下結(jié)論:
![]() ,
,![]() ,且兩個(gè)不等式中至少有一個(gè)取等號(hào),
,且兩個(gè)不等式中至少有一個(gè)取等號(hào),
①若![]() ,則必有
,則必有![]() ,∴
,∴![]() ,即對(duì)
,即對(duì)![]() ,
,![]() ,都有
,都有![]()
∴![]() ,
,![]() ,
,![]()
![]()
∴![]() ,即
,即![]() 為等差數(shù)列;
為等差數(shù)列;
②當(dāng)![]() 時(shí),則必有
時(shí),則必有![]() ,所以
,所以![]() ,即對(duì)
,即對(duì)![]() ,
,![]() ,都有
,都有![]()
∴![]() ,
,![]() ,
,![]()
![]()
所以![]() ,即
,即![]() 為等差數(shù)列;
為等差數(shù)列;
③當(dāng)![]() ,
,![]()
![]()
∵![]() ,
,![]() 中必有一個(gè)為0,∴根據(jù)上式,一個(gè)為0,則另一個(gè)亦為0,
中必有一個(gè)為0,∴根據(jù)上式,一個(gè)為0,則另一個(gè)亦為0,
即![]() ,
,![]() ,∴
,∴![]() 為常數(shù)數(shù)列,所以
為常數(shù)數(shù)列,所以![]() 為等差數(shù)列,
為等差數(shù)列,
綜上,數(shù)列![]() 也一定是等差數(shù)列.
也一定是等差數(shù)列.
(3)∵![]() ,
,
∴當(dāng)![]() 時(shí),
時(shí),![]() ,即
,即![]() ,當(dāng)
,當(dāng)![]() 時(shí),
時(shí),![]() ,即
,即![]() .
.
以下證明:![]() ,
,![]()
當(dāng)![]() 時(shí),
時(shí),
若![]() ,則
,則![]() ,
,![]() ,所以
,所以![]() ,不合題意;
,不合題意;
若![]() ,則
,則![]() ,
,![]() ,則
,則![]() ,得:
,得:![]() ,與
,與![]() 矛盾,不合題意;
矛盾,不合題意;
∴![]() ,即
,即![]() ;
;
同理可證:![]() ,即
,即![]() ,
,![]() 時(shí),
時(shí),![]() .
.
①當(dāng)![]() 時(shí),
時(shí),![]() ,
,![]() ∴
∴![]() ∴
∴![]() ,
,![]()
∵![]() ∴
∴![]()
∴![]()
![]()
②當(dāng)![]() 時(shí),
時(shí),![]() ,且
,且![]()
∴![]() ,則
,則![]() 為
為![]() 或
或![]() .若
.若![]() 為
為![]() ,則
,則![]() 為常數(shù),與題意不符,∴
為常數(shù),與題意不符,∴![]() ∴
∴![]() ∴
∴![]()
∴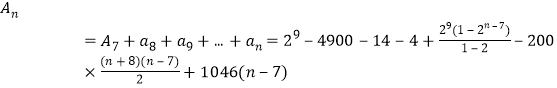
![]() ,
,
∴![]() ,
,![]() .
.


 怎樣學(xué)好牛津英語(yǔ)系列答案
怎樣學(xué)好牛津英語(yǔ)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知數(shù)列![]() 前
前![]() 項(xiàng)和為
項(xiàng)和為![]() ,且
,且![]() .
.
(1)證明數(shù)列![]() 是等比數(shù)列;
是等比數(shù)列;
(2)設(shè)![]() ,求數(shù)列
,求數(shù)列![]() 的前
的前![]() 項(xiàng)和
項(xiàng)和![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】下列說(shuō)法正確的是( )
A.若冪函數(shù)![]() 的圖象過(guò)點(diǎn)
的圖象過(guò)點(diǎn)![]() ,則
,則![]()
B.命題![]() :“
:“![]() ,
,![]() ”,則
”,則![]() 的否定為“
的否定為“![]() ,
,![]() ”
”
C.“![]() ”是“
”是“![]() ”的充分不必要條件
”的充分不必要條件
D.若![]() 與
與![]() 是相互獨(dú)立事件,則
是相互獨(dú)立事件,則![]() 與
與![]() 也是相互獨(dú)立事件
也是相互獨(dú)立事件
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知球![]() 的半徑為3,該球的內(nèi)接正三棱錐的體積最大值為
的半徑為3,該球的內(nèi)接正三棱錐的體積最大值為![]() ,內(nèi)接正四棱錐的體積最大值為
,內(nèi)接正四棱錐的體積最大值為![]() ,則
,則![]() 的值為__________.
的值為__________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】為了美化環(huán)境,某公園欲將一塊空地規(guī)劃建成休閑草坪,休閑草坪的形狀為如圖所示的四邊形ABCD.其中AB=3百米,AD=![]() 百米,且△BCD是以D為直角頂點(diǎn)的等腰直角三角形.?dāng)M修建兩條小路AC,BD(路的寬度忽略不計(jì)),設(shè)∠BAD=
百米,且△BCD是以D為直角頂點(diǎn)的等腰直角三角形.?dāng)M修建兩條小路AC,BD(路的寬度忽略不計(jì)),設(shè)∠BAD=![]() ,
,![]() (
(![]() ,
,![]() ).
).
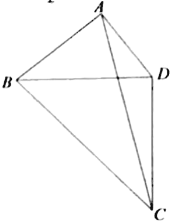
(1)當(dāng)cos![]() =
=![]() 時(shí),求小路AC的長(zhǎng)度;
時(shí),求小路AC的長(zhǎng)度;
(2)當(dāng)草坪ABCD的面積最大時(shí),求此時(shí)小路BD的長(zhǎng)度.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,將邊長(zhǎng)為2的正方形![]() 沿對(duì)角線
沿對(duì)角線![]() 折疊,使得平面
折疊,使得平面![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() .
.
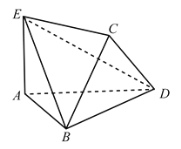
(1)若![]() ,求直線
,求直線![]() 與直線
與直線![]() 所成的角;
所成的角;
(2)若二面角![]() 的大小為
的大小為![]() ,求
,求![]() 的長(zhǎng)度.
的長(zhǎng)度.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】為了豐富學(xué)生的課外文化生活,某中學(xué)積極探索開(kāi)展課外文體活動(dòng)的新途徑及新形式,取得了良好的效果.為了調(diào)查學(xué)生的學(xué)習(xí)積極性與參加文體活動(dòng)是否有關(guān),學(xué)校對(duì)300名學(xué)生做了問(wèn)卷調(diào)查,列聯(lián)表如下:
參加文體活動(dòng) | 不參加文體活動(dòng) | 合計(jì) | |
學(xué)習(xí)積極性高 | 180 | ||
學(xué)習(xí)積極性不高 | 60 | ||
合計(jì) | 300 |
已知在全部300人中隨機(jī)抽取1人,抽到學(xué)習(xí)積極性不高的學(xué)生的概率為![]() .
.
(1)請(qǐng)將上面的列聯(lián)表補(bǔ)充完整;
(2)是否有![]() 的把握認(rèn)為學(xué)習(xí)積極性高與參加文體活動(dòng)有關(guān)?請(qǐng)說(shuō)明你的理由;
的把握認(rèn)為學(xué)習(xí)積極性高與參加文體活動(dòng)有關(guān)?請(qǐng)說(shuō)明你的理由;
(3)若從不參加文體活動(dòng)的同學(xué)中按照分層抽樣的方法選取5人,再?gòu)乃x出的5人中隨機(jī)選取2人,求至少有1人學(xué)習(xí)積極性不高的概率.
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某中藥種植基地有兩處種植區(qū)的藥材需在下周一、下周二兩天內(nèi)采摘完畢,基地員工一天可以完成一處種植區(qū)的采摘.由于下雨會(huì)影響藥材品質(zhì),基地收益如下表所示:
周一 | 無(wú)雨 | 無(wú)雨 | 有雨 | 有雨 |
周二 | 無(wú)雨 | 有雨 | 無(wú)雨 | 有雨 |
收益 |
|
|
|
|
若基地額外聘請(qǐng)工人,可在周一當(dāng)天完成全部采摘任務(wù).無(wú)雨時(shí)收益為![]() 萬(wàn)元;有雨時(shí),收益為
萬(wàn)元;有雨時(shí),收益為![]() 萬(wàn)元.額外聘請(qǐng)工人的成本為
萬(wàn)元.額外聘請(qǐng)工人的成本為![]() 萬(wàn)元.
萬(wàn)元.
已知下周一和下周二有雨的概率相同,兩天是否下雨互不影響,基地收益為![]() 萬(wàn)元的概率為
萬(wàn)元的概率為![]() .
.
(Ⅰ)若不額外聘請(qǐng)工人,寫(xiě)出基地收益![]() 的分布列及基地的預(yù)期收益;
的分布列及基地的預(yù)期收益;
(Ⅱ)該基地是否應(yīng)該外聘工人,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】北京市政府為做好![]() 會(huì)議接待服務(wù)工作,對(duì)可能遭受污染的某海產(chǎn)品在進(jìn)入餐飲區(qū)前必須進(jìn)行兩輪檢測(cè),只有兩輪都合格才能進(jìn)行銷售,否則不能銷售.已知該海產(chǎn)品第一輪檢測(cè)不合格的概率為
會(huì)議接待服務(wù)工作,對(duì)可能遭受污染的某海產(chǎn)品在進(jìn)入餐飲區(qū)前必須進(jìn)行兩輪檢測(cè),只有兩輪都合格才能進(jìn)行銷售,否則不能銷售.已知該海產(chǎn)品第一輪檢測(cè)不合格的概率為![]() ,第二輪檢測(cè)不合格的概率為
,第二輪檢測(cè)不合格的概率為![]() ,兩輪檢測(cè)是否合格相互沒(méi)有影響.
,兩輪檢測(cè)是否合格相互沒(méi)有影響.
(1)求該海產(chǎn)品不能銷售的概率.
(2)如果該海產(chǎn)品可以銷售,則每件產(chǎn)品可獲利40元;如果該海產(chǎn)品不能銷售,則每件產(chǎn)品虧損80元(即獲利-80元).已知一箱中有該海產(chǎn)品4件,記一箱該海產(chǎn)品獲利![]() 元,求
元,求![]() 的分布列,并求出數(shù)學(xué)期望
的分布列,并求出數(shù)學(xué)期望![]() .
.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com