
提高過江大橋的車輛通行能力可改善整個(gè)城市的交通狀況.在一般情況下,大橋上的車流速度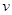 (單位:千米/小時(shí))是車流密度
(單位:千米/小時(shí))是車流密度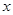 (單位:輛/千米)的函數(shù).當(dāng)橋上的車流密度達(dá)到200輛/千米時(shí),造成堵塞,此時(shí)車流速度為0千米/小時(shí);當(dāng)車流密度不超過20輛/千米時(shí),車流速度為60千米/小時(shí).研究表明:當(dāng)
(單位:輛/千米)的函數(shù).當(dāng)橋上的車流密度達(dá)到200輛/千米時(shí),造成堵塞,此時(shí)車流速度為0千米/小時(shí);當(dāng)車流密度不超過20輛/千米時(shí),車流速度為60千米/小時(shí).研究表明:當(dāng)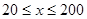 時(shí),車流速度
時(shí),車流速度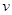 是車流密度
是車流密度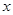 的一次函數(shù).
的一次函數(shù).
(Ⅰ)當(dāng)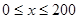 時(shí),求函數(shù)
時(shí),求函數(shù)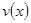 的表達(dá)式;
的表達(dá)式;
(Ⅱ)當(dāng)車流密度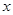 為多大時(shí),車流量(單位時(shí)間內(nèi)通過橋上某觀測點(diǎn)的車輛數(shù),單位:輛/小時(shí))
為多大時(shí),車流量(單位時(shí)間內(nèi)通過橋上某觀測點(diǎn)的車輛數(shù),單位:輛/小時(shí))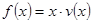 可以達(dá)到最大,并求出最大值.(精確到1輛/小時(shí)).
可以達(dá)到最大,并求出最大值.(精確到1輛/小時(shí)).
(Ⅰ)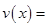
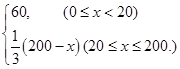 ;(Ⅱ)當(dāng)車流密度為100輛/千米時(shí),車流量可以達(dá)到最大,最大值約為3333輛/小時(shí).
;(Ⅱ)當(dāng)車流密度為100輛/千米時(shí),車流量可以達(dá)到最大,最大值約為3333輛/小時(shí).
解析試題分析:(Ⅰ)根據(jù)題意, :當(dāng)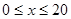 時(shí),
時(shí),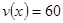 ,當(dāng)
,當(dāng)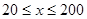 時(shí),是一次函數(shù), 可設(shè)為
時(shí),是一次函數(shù), 可設(shè)為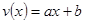 ,將
,將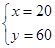 與
與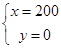 代入求出
代入求出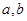 即可;(Ⅱ)分段函數(shù)最值分段求, 當(dāng)
即可;(Ⅱ)分段函數(shù)最值分段求, 當(dāng)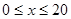 時(shí),
時(shí),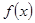 為增函數(shù),故當(dāng)
為增函數(shù),故當(dāng)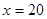 時(shí),其最大值為
時(shí),其最大值為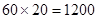 ,當(dāng)
,當(dāng)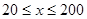 時(shí),是二次函數(shù),利用二次函數(shù)性質(zhì),求出最大值,然后比較,誰最大為誰.
時(shí),是二次函數(shù),利用二次函數(shù)性質(zhì),求出最大值,然后比較,誰最大為誰.
試題解析:(Ⅰ)由題意:當(dāng)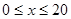 時(shí),
時(shí),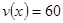 ;當(dāng)
;當(dāng)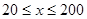 時(shí),設(shè)
時(shí),設(shè)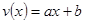 ,顯然
,顯然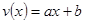 在
在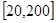 是減函數(shù),由已知得
是減函數(shù),由已知得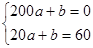 ,解得
,解得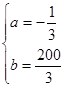 ,故函數(shù)
,故函數(shù)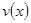 的表達(dá)式為
的表達(dá)式為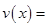
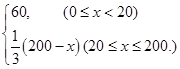
(Ⅱ)依題意并由(Ⅰ)可得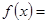
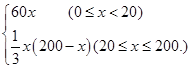 ,當(dāng)
,當(dāng)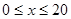 時(shí),
時(shí),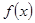 為增函數(shù),故當(dāng)
為增函數(shù),故當(dāng)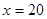 時(shí),其最大值為
時(shí),其最大值為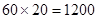 ;當(dāng)
;當(dāng)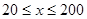 時(shí),
時(shí), ,當(dāng)且僅當(dāng)
,當(dāng)且僅當(dāng)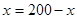 ,即
,即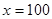 時(shí),等號成立.所以,當(dāng)
時(shí),等號成立.所以,當(dāng)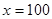 時(shí),
時(shí),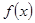 在區(qū)間
在區(qū)間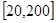 上取得最大值
上取得最大值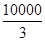 .
.
綜上,當(dāng)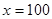 時(shí),
時(shí),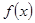 在區(qū)間
在區(qū)間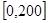 上取得最大值
上取得最大值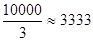 ,
,
即當(dāng)車流密度為100輛/千米時(shí),車流量可以達(dá)到最大,最大值約為3333輛/小時(shí).
考點(diǎn):1、求函數(shù)解析式, 2、求二次函數(shù)最大值.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù) 圖象上一點(diǎn)
圖象上一點(diǎn) 處的切線方程為
處的切線方程為 .
.
(1)求 的值;
的值;
(2)若方程 在
在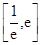 內(nèi)有兩個(gè)不等實(shí)根,求
內(nèi)有兩個(gè)不等實(shí)根,求 的取值范圍(其中
的取值范圍(其中 為自然對數(shù)的底數(shù));(3)令
為自然對數(shù)的底數(shù));(3)令 ,若
,若 的圖象與
的圖象與 軸交于
軸交于 (其中
(其中 ),
), 的中點(diǎn)為
的中點(diǎn)為 ,求證:
,求證: 在
在 處的導(dǎo)數(shù)
處的導(dǎo)數(shù)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,在半徑為 、圓心角為
、圓心角為 的扇形的弧上任取一點(diǎn)
的扇形的弧上任取一點(diǎn) ,作扇形的內(nèi)接矩形
,作扇形的內(nèi)接矩形 ,使點(diǎn)
,使點(diǎn) 在
在 上,點(diǎn)
上,點(diǎn) 在
在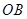 上,設(shè)矩形
上,設(shè)矩形 的面積為
的面積為 ,
,
(Ⅰ)按下列要求求出函數(shù)關(guān)系式:
①設(shè) ,將
,將 表示成
表示成 的函數(shù)關(guān)系式;
的函數(shù)關(guān)系式;
②設(shè) ,將
,將 表示成
表示成 的函數(shù)關(guān)系式;
的函數(shù)關(guān)系式;
(Ⅱ)請你選用(1)中的一個(gè)函數(shù)關(guān)系式,求出 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分13分)某沿海地區(qū)養(yǎng)殖的一種特色海鮮上市時(shí)間僅能持續(xù)5個(gè)月,預(yù)測上市初期和后期會(huì)因供應(yīng)不足使價(jià)格呈持續(xù)上漲態(tài)勢,而中期又將出現(xiàn)供大于求,使價(jià)格連續(xù)下跌.現(xiàn)有三種價(jià)格模擬函數(shù):①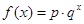 ;②
;②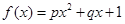 ;③
;③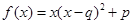 .(以上三式中
.(以上三式中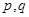 均為常數(shù),且
均為常數(shù),且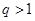 )
)
(1)為準(zhǔn)確研究其價(jià)格走勢,應(yīng)選哪種價(jià)格模擬函數(shù)(不必說明理由)
(2)若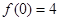 ,
,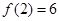 ,求出所選函數(shù)
,求出所選函數(shù) 的解析式(注:函數(shù)定義域是
的解析式(注:函數(shù)定義域是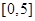 .其中
.其中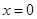 表示8月1日,
表示8月1日,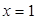 表示9月1日,…,以此類推);
表示9月1日,…,以此類推);
(3)在(2)的條件下研究下面課題:為保證養(yǎng)殖戶的經(jīng)濟(jì)效益,當(dāng)?shù)卣?jì)劃在價(jià)格下跌期間積極拓寬外銷,請你預(yù)測該海鮮將在哪幾個(gè)月份內(nèi)價(jià)格下跌.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
某工廠某種產(chǎn)品的年固定成本為250萬元,每生產(chǎn) 千件,需另投入成本為
千件,需另投入成本為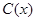 ,當(dāng)年產(chǎn)量不足80千件時(shí),
,當(dāng)年產(chǎn)量不足80千件時(shí), (萬元).當(dāng)年產(chǎn)量不小于80千件時(shí),
(萬元).當(dāng)年產(chǎn)量不小于80千件時(shí), (萬元).每件商品售價(jià)為0.05萬元.通過市場分析,該廠生產(chǎn)的商品能全部售完.
(萬元).每件商品售價(jià)為0.05萬元.通過市場分析,該廠生產(chǎn)的商品能全部售完.
(Ⅰ)寫出年利潤 (萬元)關(guān)于年產(chǎn)量
(萬元)關(guān)于年產(chǎn)量 (千件)的函數(shù)解析式;
(千件)的函數(shù)解析式;
(Ⅱ)年產(chǎn)量為多少千件時(shí),該廠在這一商品的生產(chǎn)中所獲利潤最大?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù)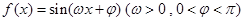 在一個(gè)周期內(nèi)的部分對應(yīng)值如下表:
在一個(gè)周期內(nèi)的部分對應(yīng)值如下表:
 | 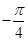 |  | 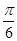 |  | 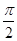 | 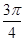 |
 |  |  | 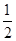 |  | 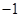 |  |
 的解析式;
的解析式;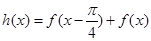 ,
,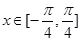 ,求
,求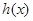 的最大值和最小值.
的最大值和最小值.查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù)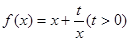 和點(diǎn)
和點(diǎn) ,過點(diǎn)
,過點(diǎn) 作曲線
作曲線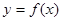 的兩條切線
的兩條切線 、
、 ,切點(diǎn)分別為
,切點(diǎn)分別為 、
、 .
.
(Ⅰ)設(shè)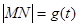 ,試求函數(shù)
,試求函數(shù) 的表達(dá)式;
的表達(dá)式;
(Ⅱ)是否存在 ,使得
,使得 、
、 與
與 三點(diǎn)共線.若存在,求出
三點(diǎn)共線.若存在,求出 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
(Ⅲ)在(Ⅰ)的條件下,若對任意的正整數(shù)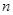 ,在區(qū)間
,在區(qū)間 內(nèi)總存在
內(nèi)總存在 個(gè)實(shí)數(shù)
個(gè)實(shí)數(shù)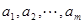 ,
, ,使得不等式
,使得不等式 成立,求
成立,求 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
對于在區(qū)間 [ m,n ] 上有意義的兩個(gè)函數(shù) 與
與 ,如果對任意
,如果對任意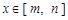 ,均有
,均有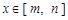 ,則稱
,則稱 與
與 在 [ m,n ] 上是友好的,否則稱
在 [ m,n ] 上是友好的,否則稱 與
與 在 [ m,n ]是不友好的.現(xiàn)有兩個(gè)函數(shù)
在 [ m,n ]是不友好的.現(xiàn)有兩個(gè)函數(shù) 與
與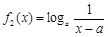 (a > 0且
(a > 0且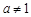 ),給定區(qū)間
),給定區(qū)間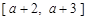 .
.
(1)若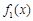 與
與 在給定區(qū)間
在給定區(qū)間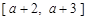 上都有意義,求a的取值范圍;
上都有意義,求a的取值范圍;
(2)討論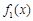 與
與 在給定區(qū)間
在給定區(qū)間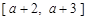 上是否友好.
上是否友好.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com