
【題目】已知橢圓C:![]() +
+![]() =1(a>b>0)經過點(1,
=1(a>b>0)經過點(1,![]() ),且焦距為2
),且焦距為2![]() .
.
(1)求橢圓C方程;
(2)橢圓C的左,右焦點分別為F1,F2,過點F2的直線l與橢圓C交于A,B兩點,求△F2AB面積S的最大值并求出相應直線l的方程.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]()
【解析】
(1)將點![]() 代入橢圓方程得
代入橢圓方程得![]() ,又焦距為
,又焦距為![]() ,故得
,故得![]() ,進而根據
,進而根據![]() 得
得![]() 的值;
的值;
(2)設直線l的方程為x=my+![]() ,借助韋達定理,用m表示出三角形△F2AB面積,利用基本不等式求出最大值,進而得出直線方程。
,借助韋達定理,用m表示出三角形△F2AB面積,利用基本不等式求出最大值,進而得出直線方程。
解:(1)由已知可得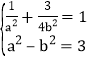 ,解得a2=4,b2=1,
,解得a2=4,b2=1,
∴橢圓C方程為![]() +y2=1,
+y2=1,
(2)由題中左、右焦點易知F1(-![]() ,0),F2(-
,0),F2(-![]() ,0),
,0),
若直線l的傾斜角為0,顯然F,A,B三點不構成三角形,
故直線l的傾斜角不為0,可設直線l的方程為x=my+![]() ,
,
由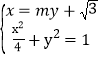 ,
,
消x可得(m2+4)y2+2![]() my-1=0.
my-1=0.
設A(x1,y1)、B(x2,y2),
則y1+y2= -![]() ,y1y2= -
,y1y2= -![]() .
.
∴|y1-y2|=![]() ═
═![]() =
=![]() .
.
∴△F2AB的面積S=![]() |F1F2||y1-y2|=4
|F1F2||y1-y2|=4![]()
![]() =4
=4![]()
![]()
=4![]()
![]() ≤4
≤4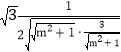 =2.
=2.
當且僅當m2+1=3,即m=±![]() 時,等號成立,S取得最大值2,
時,等號成立,S取得最大值2,
此時直線l的方程為x+![]() y-
y-![]() =0,或x-
=0,或x-![]() y-
y-![]() =0.
=0.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】某工廠用7萬元錢購買了一臺新機器,運輸安裝費用2千元,每年投保、動力消耗的費用也為2千元,每年的保養、維修、更換易損零件的費用逐年增加,第一年為2千元,第二年為3千元,第三年為4千元,依此類推,即每年增加1千元.
(1)求使用n年后,保養、維修、更換易損零件的累計費用S(千元)關于n的表達式;
(2)問這臺機器最佳使用年限是多少年?并求出年平均費用(單位:千元)的最小值.(最佳使用年限是指使年平均費用最小的時間,年平均費用=(購入機器費用+運輸安裝費用+每年投保、動力消耗的費用+保養、維修、更換易損零件的累計費用)÷機器使用的年數)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】過原點的一條直線與橢圓![]() =1(a>b>0)交于A,B兩點,以線段AB為直徑的圓過該橢圓的右焦點F2,若∠ABF2∈[
=1(a>b>0)交于A,B兩點,以線段AB為直徑的圓過該橢圓的右焦點F2,若∠ABF2∈[![]() ],則該橢圓離心率的取值范圍為( )
],則該橢圓離心率的取值范圍為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】3月12日,全國政協總工會界別小組會議上,人社部副部長湯濤在回應委員呼聲時表示無論是從養老金方面,還是從人力資源的合理配置來說,延遲退休是大勢所趨.不過,湯部長也表示,不少職工對于延遲退休有著不同的意見.某高校一社團就是否同意延遲退休的情況隨機采訪了200名市民,并進行了統計,得到如下的![]() 列聯表:
列聯表:
贊同延遲退休 | 不贊同延遲退休 | 合計 | |
男性 | 80 | 20 | 100 |
女性 | 60 | 40 | 100 |
合計 | 140 | 60 | 200 |
(1)根據上面的列聯表判斷能否有![]() 的把握認為對延遲退休的態度與性別有關;
的把握認為對延遲退休的態度與性別有關;
(2)為了進一步征求對延遲退休的意見和建議,從抽取的200位市民中對不贊同的按照分層抽樣的方法抽取6人,再從這6人中隨機抽出3名進行電話回訪,求3人中至少有1人為男性的概率.
附: 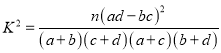 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 是公差不為零的等差數列,滿足
是公差不為零的等差數列,滿足![]() ,且
,且![]() 、
、![]() 、
、![]() 成等比數列.
成等比數列.
(1)求數列![]() 的通項公式;
的通項公式;
(2)設數列![]() 滿足
滿足![]() ,求數列
,求數列![]() 的前
的前![]() 項和
項和![]() .
.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】試題分析:(1)設等差數列![]() 的公差為
的公差為![]() ,由a3=7,且
,由a3=7,且![]() 、
、![]() 、
、![]() 成等比數列.可得
成等比數列.可得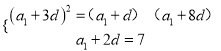 ,解之得即可得出數列
,解之得即可得出數列![]() 的通項公式;
的通項公式;
2)由(1)得![]() ,則
,則![]() ,由裂項相消法可求數列
,由裂項相消法可求數列![]() 的前
的前![]() 項和
項和![]() .
.
試題解析:(1)設數列![]() 的公差為
的公差為![]() ,且
,且![]() 由題意得
由題意得![]() ,
,
即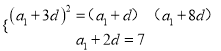 ,解得
,解得![]() ,
,
所以數列![]() 的通項公式
的通項公式![]() .
.
(2)由(1)得![]()
![]() ,
,
![]()
![]() .
.
【題型】解答題
【結束】
18
【題目】四棱錐![]() 的底面
的底面![]() 為直角梯形,
為直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() 為正三角形.
為正三角形.
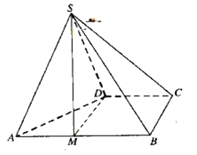
(1)點![]() 為棱
為棱![]() 上一點,若
上一點,若![]() 平面
平面![]() ,
,![]() ,求實數
,求實數![]() 的值;
的值;
(2)求點B到平面SAD的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《中華人民共和國道路交通安全法》第47條的相關規定:機動車行經人行道時,應當減速慢行;遇行人正在通過人行道,應當停車讓行,俗稱“禮讓斑馬線”, 《中華人民共和國道路交通安全法》第90條規定:對不禮讓行人的駕駛員處以扣3分,罰款50元的處罰.下表是某市一主干路口監控設備所抓拍的5個月內駕駛員“禮讓斑馬線”行為統計數據:
月份 | 1 | 2 | 3 | 4 | 5 |
違章駕駛員人數 | 120 | 105 | 100 | 90 | 85 |
(1)請利用所給數據求違章人數![]() 與月份
與月份![]() 之間的回歸直線方程
之間的回歸直線方程![]() ;
;
(2)預測該路口9月份的不“禮讓斑馬線”違章駕駛員人數.
參考公式:  ,
, ![]() .
.
參考數據: ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,以橢圓
,以橢圓![]() 的任意三個頂點為頂點的三角形的面積是
的任意三個頂點為頂點的三角形的面積是![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設![]() 是橢圓
是橢圓![]() 的右頂點,點
的右頂點,點![]() 在
在![]() 軸上.若橢圓
軸上.若橢圓![]() 上存在點
上存在點![]() ,使得
,使得![]() ,求點
,求點![]() 橫坐標的取值范圍.
橫坐標的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com