
【題目】已知![]() ,函數(shù)
,函數(shù)![]() .
.
(1)若![]() ,證明:函數(shù)
,證明:函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上是單調(diào)增函數(shù);
上是單調(diào)增函數(shù);
(2)求函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的最大值;
上的最大值;
(3)若函數(shù)![]() 的圖像過原點,且
的圖像過原點,且![]() 的導(dǎo)數(shù)
的導(dǎo)數(shù)![]() ,當(dāng)
,當(dāng)![]() 時,函數(shù)
時,函數(shù)![]() 過點
過點![]() 的切線至少有2條,求實數(shù)
的切線至少有2條,求實數(shù)![]() 的值.
的值.
【答案】(1)證明見解析;(2)當(dāng)![]() 時,最大值為
時,最大值為![]() ;當(dāng)
;當(dāng)![]() 時,最大值為
時,最大值為![]() (3)
(3)![]()
【解析】
(1)由題![]() ,利用導(dǎo)函數(shù)求單調(diào)區(qū)間即可;
,利用導(dǎo)函數(shù)求單調(diào)區(qū)間即可;
(2)利用導(dǎo)數(shù)可以推導(dǎo)得到![]() 在區(qū)間
在區(qū)間![]() 上是減函數(shù),在區(qū)間
上是減函數(shù),在區(qū)間![]() 上是增函數(shù),則當(dāng)
上是增函數(shù),則當(dāng)![]() 時,
時,![]() 的最大值為
的最大值為![]() 和
和![]() 中的最大值,作差可得
中的最大值,作差可得![]() ,設(shè)
,設(shè)![]() ,再次利用導(dǎo)數(shù)推導(dǎo)
,再次利用導(dǎo)數(shù)推導(dǎo)![]() 的單調(diào)性,進(jìn)而得到
的單調(diào)性,進(jìn)而得到![]() 上的最大值;
上的最大值;
(3)由題可得![]() ,設(shè)切點為
,設(shè)切點為![]() ,則
,則![]() 處的切線方程為:
處的切線方程為:![]() ,將
,將![]() 代入可得
代入可得![]() ,則將原命題等價為關(guān)于
,則將原命題等價為關(guān)于![]() 的方程至少有2個不同的解,設(shè)
的方程至少有2個不同的解,設(shè)![]() ,進(jìn)而利用導(dǎo)函數(shù)判斷
,進(jìn)而利用導(dǎo)函數(shù)判斷![]() 的單調(diào)性,從而求解即可
的單調(diào)性,從而求解即可
(1)證明:![]() ,則
,則![]() ,
,
![]() 當(dāng)
當(dāng)![]() 時,
時,![]() ,
,
![]()
![]() ,即此時函數(shù)
,即此時函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上是單調(diào)增函數(shù).
上是單調(diào)增函數(shù).
(2)由(1)知,當(dāng)![]() 時,函數(shù)
時,函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上是單調(diào)增函數(shù),
上是單調(diào)增函數(shù),
當(dāng)![]() 時,
時,![]() ,則
,則![]() ,
,![]() ,則
,則![]() 在區(qū)間
在區(qū)間![]() 上是單調(diào)減函數(shù);
上是單調(diào)減函數(shù);
同理,當(dāng)![]() 時,
時,![]() 在區(qū)間
在區(qū)間![]() 上是單調(diào)增函數(shù),在區(qū)間
上是單調(diào)增函數(shù),在區(qū)間![]() 上是單調(diào)減函數(shù);
上是單調(diào)減函數(shù);
即當(dāng)![]() ,且
,且![]() 時,
時,![]() 在區(qū)間
在區(qū)間![]() 上是減函數(shù),在區(qū)間
上是減函數(shù),在區(qū)間![]() 上是增函數(shù),
上是增函數(shù),
則當(dāng)![]() 時,
時,![]() 的最大值為
的最大值為![]() 和
和![]() 中的最大值,
中的最大值,
![]() ,
,
![]() 令
令![]() ,
,
則 ,
,
![]()
![]() 在
在![]() 上為增函數(shù),
上為增函數(shù),
![]() ,
,
![]() 當(dāng)
當(dāng)![]() 時,
時,![]() ,即
,即![]() ,此時最大值為
,此時最大值為![]() ;
;
當(dāng)![]() 時,
時,![]() ,即
,即![]() ,此時最大值為
,此時最大值為![]() .
.
(3)![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() 的圖像過原點,
的圖像過原點,
![]() ,即
,即![]() ,則
,則![]() ,
,
設(shè)切點為![]() ,則
,則![]() 處的切線方程為:
處的切線方程為:![]() ,
,
將![]() 代入得
代入得![]() ,
,
即![]() (※),
(※),
則原命題等價為關(guān)于![]() 的方程(※)至少有2個不同的解,
的方程(※)至少有2個不同的解,
設(shè)![]() ,
,
則![]() ,
,
令![]() ,
,![]() ,
,
![]() ,
,
當(dāng)![]() 和
和![]() 時,
時,![]() ,此時函數(shù)
,此時函數(shù)![]() 為增函數(shù);
為增函數(shù);
當(dāng)![]() 時,
時,![]() ,此時函數(shù)
,此時函數(shù)![]() 減函數(shù),
減函數(shù),
![]()
![]() 的極大值為
的極大值為![]() ,
,
![]() 的極小值為
的極小值為![]() ,
,
設(shè)![]() ,則
,則![]() ,則原命題等價為
,則原命題等價為![]() ,即
,即![]() 對
對![]() 恒成立,
恒成立,
![]() 由
由![]() 得
得![]() ,
,
設(shè)![]() ,則
,則![]() ,
,
令![]() ,則
,則![]() ,
,![]() ,當(dāng)
,當(dāng)![]() 時,
時,![]() ;當(dāng)
;當(dāng)![]() 時,
時,![]() ,
,
即![]() 在
在![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 上單調(diào)遞減,
上單調(diào)遞減,
![]() 的最大值為
的最大值為![]() ,
,![]()
![]() ,
,
故![]() ,
,
綜上所述,當(dāng)![]() 時,函數(shù)
時,函數(shù)![]() 過點
過點![]() 的切線至少有2條,此時實數(shù)m的值為
的切線至少有2條,此時實數(shù)m的值為![]()


科目:高中數(shù)學(xué) 來源: 題型:
【題目】為評估設(shè)備![]() 生產(chǎn)某種零件的性能,從設(shè)備
生產(chǎn)某種零件的性能,從設(shè)備![]() 生產(chǎn)零件的流水線上隨機抽取100件零件作為樣本,測量其直徑后,整理得到下表:
生產(chǎn)零件的流水線上隨機抽取100件零件作為樣本,測量其直徑后,整理得到下表:

經(jīng)計算,樣本的平均值![]() ,標(biāo)準(zhǔn)差
,標(biāo)準(zhǔn)差![]() ,以頻率值作為概率的估計值.
,以頻率值作為概率的估計值.
(1)為評判一臺設(shè)備的性能,從該設(shè)備加工的零件中任意抽取一件,記其直徑為![]() ,并根據(jù)以下不等式進(jìn)行評判(
,并根據(jù)以下不等式進(jìn)行評判(![]() 表示相應(yīng)事件的概率);①
表示相應(yīng)事件的概率);①![]() ;②
;②![]() ;③
;③![]() ,評判規(guī)則為:若同時滿足上述三個不等式,則設(shè)備等級為甲;僅滿足其中兩個,則等級為乙;若僅滿足其中一個,則等級為丙;若全部不滿足,則等級為丁,試判斷設(shè)備
,評判規(guī)則為:若同時滿足上述三個不等式,則設(shè)備等級為甲;僅滿足其中兩個,則等級為乙;若僅滿足其中一個,則等級為丙;若全部不滿足,則等級為丁,試判斷設(shè)備![]() 的性能等級.
的性能等級.
(2)將直徑小于等于![]() 或直徑大于
或直徑大于![]() 的零件認(rèn)為是次品.
的零件認(rèn)為是次品.
(ⅰ)若從設(shè)備![]() 的生產(chǎn)流水線上隨意抽取
的生產(chǎn)流水線上隨意抽取![]() 件零件,求恰有一件次品的概率;
件零件,求恰有一件次品的概率;
(ⅱ)若從樣本中隨意抽取![]() 件零件,計算其中次品個數(shù)
件零件,計算其中次品個數(shù)![]() 的分布列和數(shù)學(xué)期望
的分布列和數(shù)學(xué)期望![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,四棱錐![]() 中,底面
中,底面![]() 是平行四邊形,平面
是平行四邊形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() 在
在![]() 上.
上.
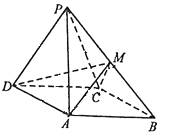
(1)若點![]() 是
是![]() 的中點,求證:
的中點,求證:![]() 平面
平面![]() ;
;
(2)在線段![]() 上確定點
上確定點![]() 的位置,使得二面角
的位置,使得二面角![]() 的余弦值為
的余弦值為![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為了檢驗訓(xùn)練情況,武警某支隊于近期舉辦了一場展示活動,其中男隊員12人,女隊員18人,測試結(jié)果如莖葉圖所示(單位:分).若成績不低于175分者授予“優(yōu)秀警員”稱號,其他隊員則給予“優(yōu)秀陪練員”稱號.
(1)若用分層抽樣的方法從“優(yōu)秀警員”和“優(yōu)秀陪練員”中共提取10人,然后再從這10人中選4人,那么至少有1人是“優(yōu)秀警員”的概率是多少?
(2)若所有“優(yōu)秀警員”中選3名代表,用![]() 表示所選女“優(yōu)秀警員”的人數(shù),試求
表示所選女“優(yōu)秀警員”的人數(shù),試求![]() 的分布列和數(shù)學(xué)期望.
的分布列和數(shù)學(xué)期望.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下圖是我國2008年至2014年生活垃圾無害化處理量(單位:億噸)的折線圖.
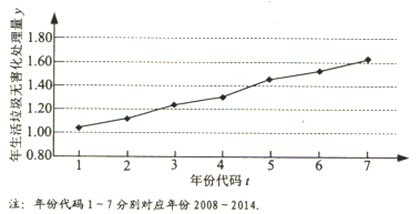
(Ⅰ)由折線圖看出,可用線性回歸模型擬合y與t的關(guān)系,請用相關(guān)系數(shù)加以說明;
(Ⅱ)建立y關(guān)于t的回歸方程(系數(shù)精確到0.01),預(yù)測2016年我國生活垃圾無害化處理量.
附注:
參考數(shù)據(jù):![]() ,
,![]() ,
,
![]() ,
,![]() ≈2.646.
≈2.646.
參考公式:相關(guān)系數(shù)
回歸方程![]() 中斜率和截距的最小二乘估計公式分別為:
中斜率和截距的最小二乘估計公式分別為:
![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,其圖象關(guān)于直線
,其圖象關(guān)于直線![]() 對稱,為了得到函數(shù)
對稱,為了得到函數(shù)![]() 的圖象,只需將函數(shù)
的圖象,只需將函數(shù)![]() 的圖象上的所有點( )
的圖象上的所有點( )
A.先向左平移![]() 個單位長度,再把所得各點橫坐標(biāo)伸長為原來的2倍,縱坐標(biāo)保持不變
個單位長度,再把所得各點橫坐標(biāo)伸長為原來的2倍,縱坐標(biāo)保持不變
B.先向右平移![]() 個單位長度,再把所得各點橫坐標(biāo)縮短為原來的
個單位長度,再把所得各點橫坐標(biāo)縮短為原來的![]() ,縱坐標(biāo)保持不變
,縱坐標(biāo)保持不變
C.先向右平移![]() 個單位長度,再把所得各點橫坐標(biāo)伸長為原來的2倍,縱坐標(biāo)保持不變
個單位長度,再把所得各點橫坐標(biāo)伸長為原來的2倍,縱坐標(biāo)保持不變
D.先向左平移![]() 個單位長度,再把所得各點橫坐標(biāo)縮短為原來的
個單位長度,再把所得各點橫坐標(biāo)縮短為原來的![]() ,縱坐標(biāo)保持不變
,縱坐標(biāo)保持不變
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某冰糖橙,甜橙的一種,云南著名特產(chǎn),以味甜皮薄著稱。該橙按照等級可分為四類:珍品、特級、優(yōu)級和一級(每箱有5kg),某采購商打算訂購一批橙子銷往省外,并從采購的這批橙子中隨機抽取100箱,利用橙子的等級分類標(biāo)準(zhǔn)得到的數(shù)據(jù)如下表:
等級 | 珍品 | 特級 | 優(yōu)級 | 一級 |
箱數(shù) | 40 | 30 | 10 | 20 |
(1)若將頻率改為概率,從這100箱橙子中有放回地隨機抽取4箱,求恰好抽到2箱是一級品的概率:
(2)利用樣本估計總體,莊園老板提出兩種購銷方案供采購商參考:
方案一:不分等級賣出,價格為27元/kg;
方案二:分等級賣出,分等級的橙子價格如下:
等級 | 珍品 | 特級 | 優(yōu)級 | 一級 |
售價(元/kg) | 36 | 30 | 24 | 18 |
從采購商的角度考慮,應(yīng)該采用哪種方案?
(3)用分層抽樣的方法從這100箱橙子中抽取10箱,再從抽取的10箱中隨機抽取3箱,X表示抽取的是珍品等級,求x的分布列及數(shù)學(xué)期望E(X).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】高考數(shù)學(xué)考試中有12道選擇題,每道選擇題有4個選項,其中有且僅有一個是正確的.評分標(biāo)準(zhǔn)規(guī)定:在每小題給出的四個選項中,只有一項是符合題目要求的,答對得5分,不答或答錯得0分.某考生每道選擇題都選出一個答案,能確定其中有8道題的答案是正確的,而其余題中,有兩道題都可判斷出兩個選項是錯誤的,有一道題能判斷出一個選項是錯誤的,還有一道題因不理解題意只能亂猜.試求該考生的選擇題:
(1)得60分的概率;
(2)得多少分的概率最大?
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com